
中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
まず先に,中心角を求める。 面積を求める式を使い, 中心角をa°として 方程式をつくる。 おうぎ形の面積 = 半径 × 半径 × π × 中心角 360° この式に 面積11π,半径=6, 中心角aを代入すると 11π = 36π × a 360 a = 11×360÷36 = 110 よって, 中心角110° 扇形の面積や弧の長さは中心角に比例します。 半径をr、中心角をθ、円周率をπとすると (1)面積(Sとします) S=πr^2*θ/360 (2)弧の長さ(Lとします) L=2πrθ/360 これらを変形してθ=の形にすればOKです。
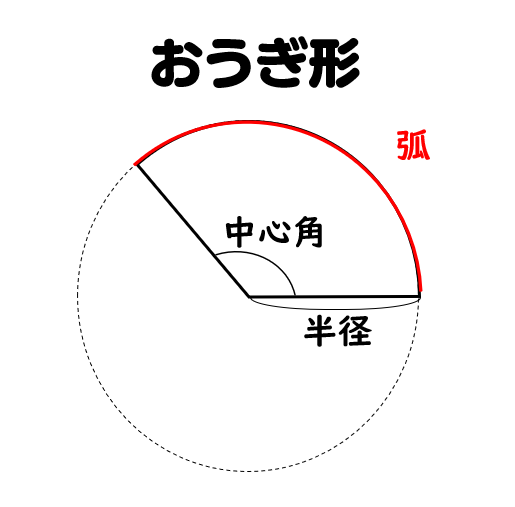
おうぎ形 中心角 求め方 半径と面積
おうぎ形 中心角 求め方 半径と面積-こうして、中心角が240°と計算できます。 練習問題:扇形(おうぎ形)の弧の長さと面積を出す Q1 次の問題を解きましょう 半径が6cm、弧の長さが$2π$の扇形について、中心角と面積を求めましょう。 A1 解答 先に中心角を計算します。中心角を\(x\)とする 扇形の面積 求めたい半径の大きさを ㎝とすると 半径が ㎝で中心角が1°の扇形の面積は と、表すことができます。 そして、面積が ㎠になるはずだから という二次方程式が完成します。 あとは、これを解いていけば の値(半径)を求めることができ

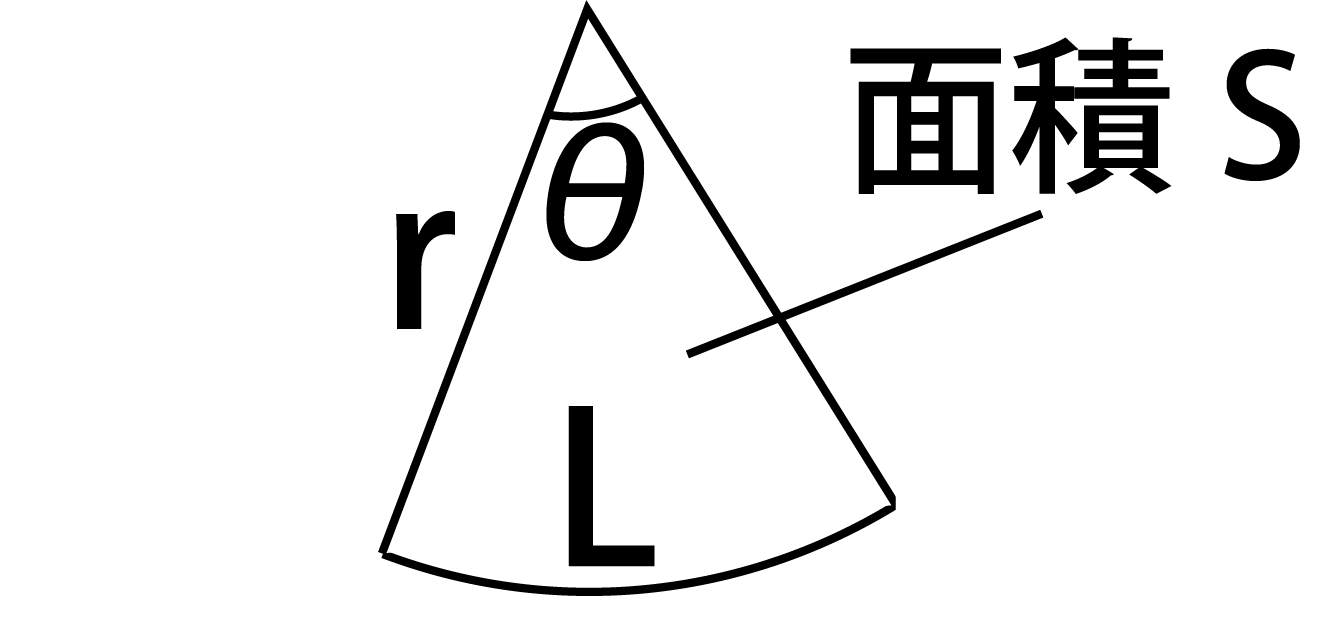
円錐の側面積 展開図の扇形の中心角 半径 母線を軸として解く 身勝手な主張
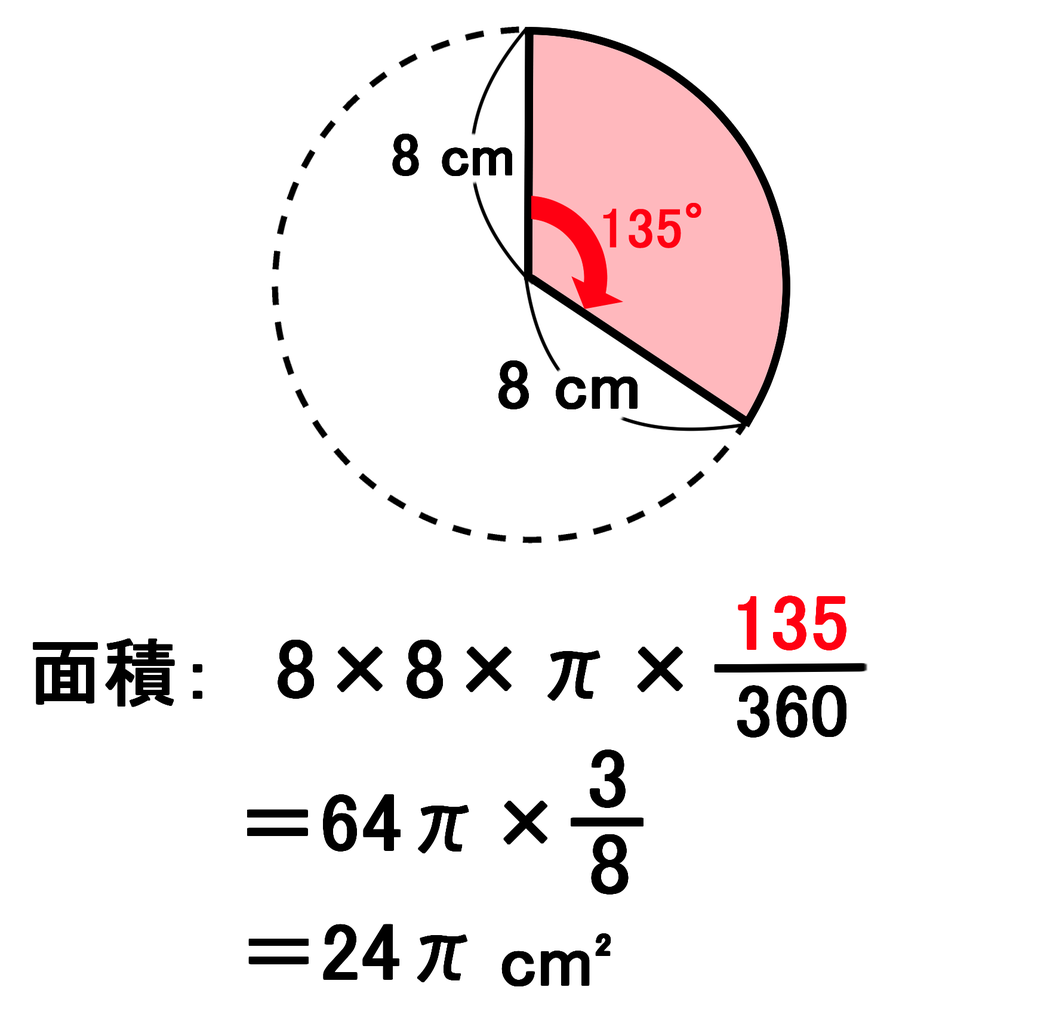
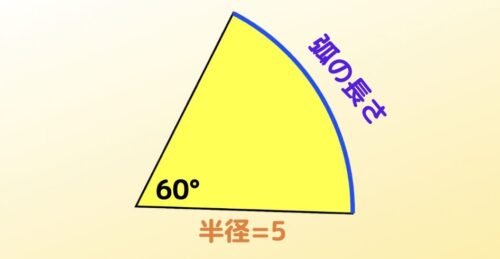
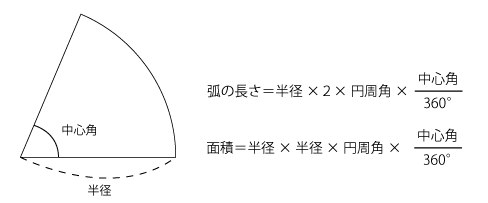
やった「おうぎ形とバームクーヘン」も、平均を利用している。 ー下のように、「長方形のまわりを円がすべらないように一周ころがった ときに、円が通った部分の面積を求めなさい」という問題では、 面積=円の中心が通った部分の長さ×円の直径同様に、中心角 2° の扇形の面積は、半径が等しい円の面積の360分の2、となるわけですね。 公式の2行目に書いた通り、扇形の面積は、半径 r と弧の長さ l が分かっている場合、次の式で簡単に求められてしまいます。面積を求めよ。 半径 18 5 cm, 中心角125°のおうぎ形がある。 弧の長さを求めよ。 面積を求めよ。 半径8cm, 中心角405°のおうぎ形がある。 弧の長さを求めよ。 面積を求めよ。 pdfファイル 解説ページに解説がない問題で、解説をご希望の場合は
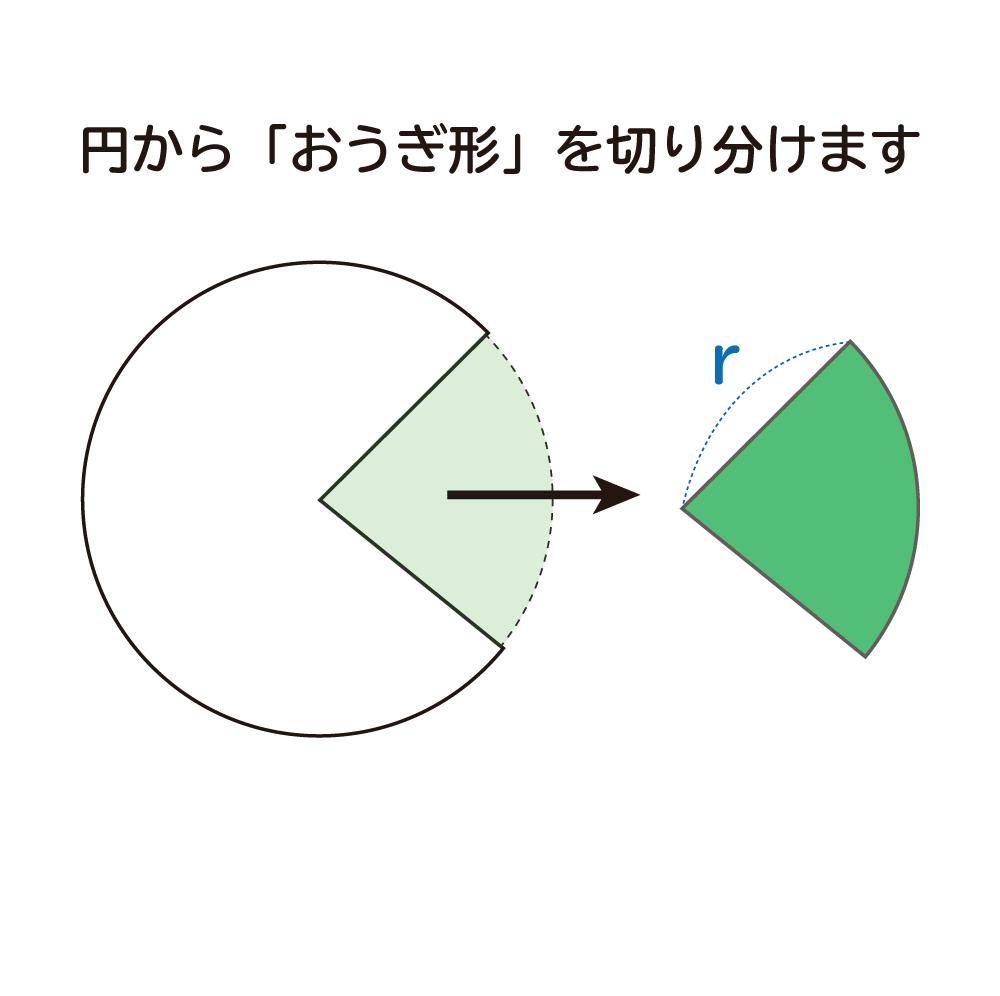
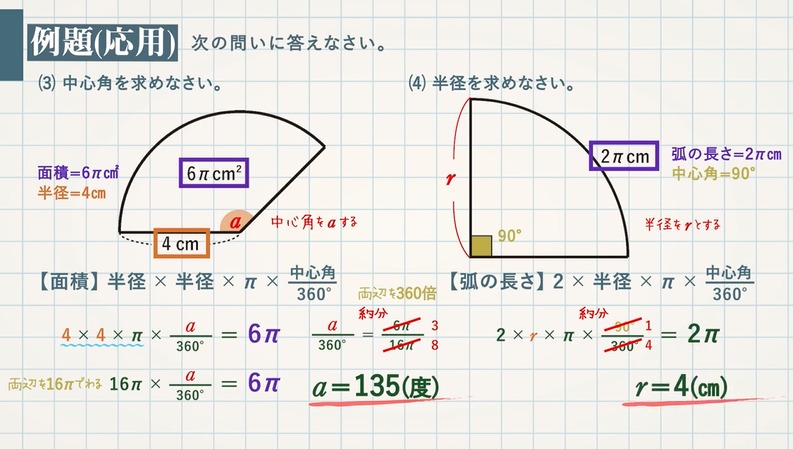
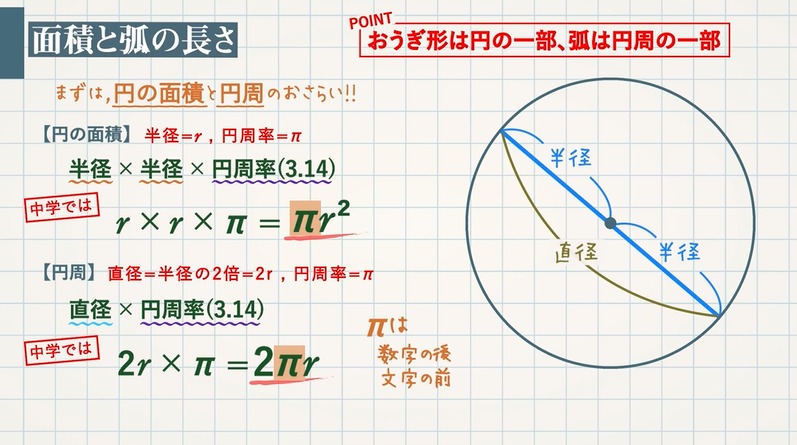
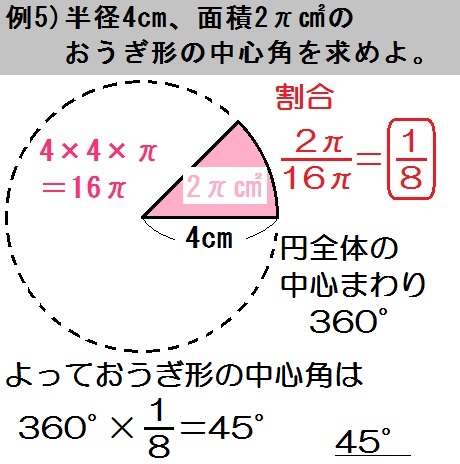
基本的なおうぎ形の面積の出し方 与えられている長さが「対角線」ではなく「直径や半径」なら学校授業の難度です。 円を4等分した形に見えますので、まずは分割する前の状態に戻してみます。 まずはこの図から「円」の面積を求めてみます。円の面積から半径 扇形の面積 弓形の面積(中心角から) 弓形の面積(弓形の半径と高さから) 弓形の面積(弓形の弦長と高さから) 楕円の面積 楕円扇形の面積 楕円弓形の面積 放物線の弓形 双曲線弓形の面積 双曲線扇形の面積 地図をなぞって面積 おうぎ形の半径と面積から、中心角を求める式を教えて下さいm(__)m※急ぎです! 半径×半径×πで円の面積をだし、扇形の面積÷その円の面積の面積を計算してその答え×360で中心角が出ます 半径4cm 面積6πcm²の扇形の中心角の求め方を教えてください。 弧
おうぎ形 中心角 求め方 半径と面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「おうぎ形 中心角 求め方 半径と面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |
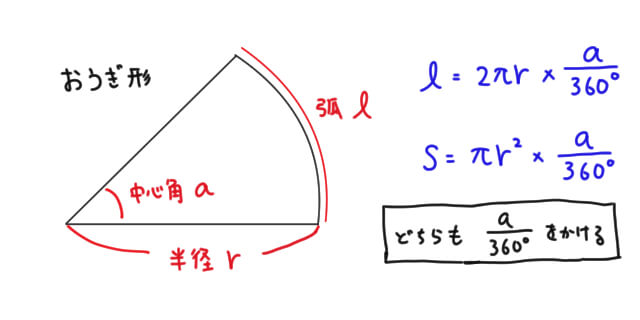
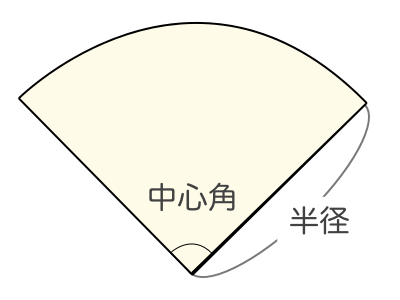
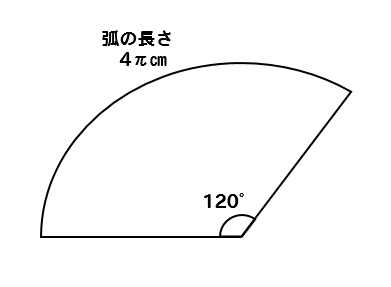
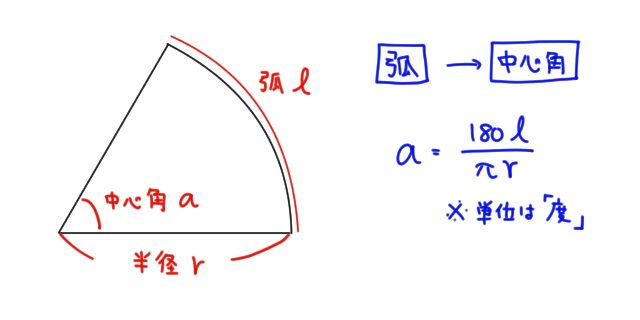
おうぎ形の中心角の求め方は次のとおり。 おうぎ形の中心角の公式は次のとおり。 求め方を見ていきましょう。 おうぎ形の半径\ (r\)と弧の長さ\ (l\)が分かるときは、公式\ (\frac {l} {\pi r}\times180^\circ\)を使って中心角を求めます。 半径が\ (6\)\ (\mathrm {cm a×d=b×c という形になるね。 これをおうぎ形に使ってみよう。 おうぎ形で比例式を使うときは、調べたいおうぎ形と半径が同じ円を考えましょう。 つまり、 この2つで考えるということですね。 作る比例式は、以下になります。
Incoming Term: おうぎ形 中心角 求め方 半径と面積,




0 件のコメント:
コメントを投稿