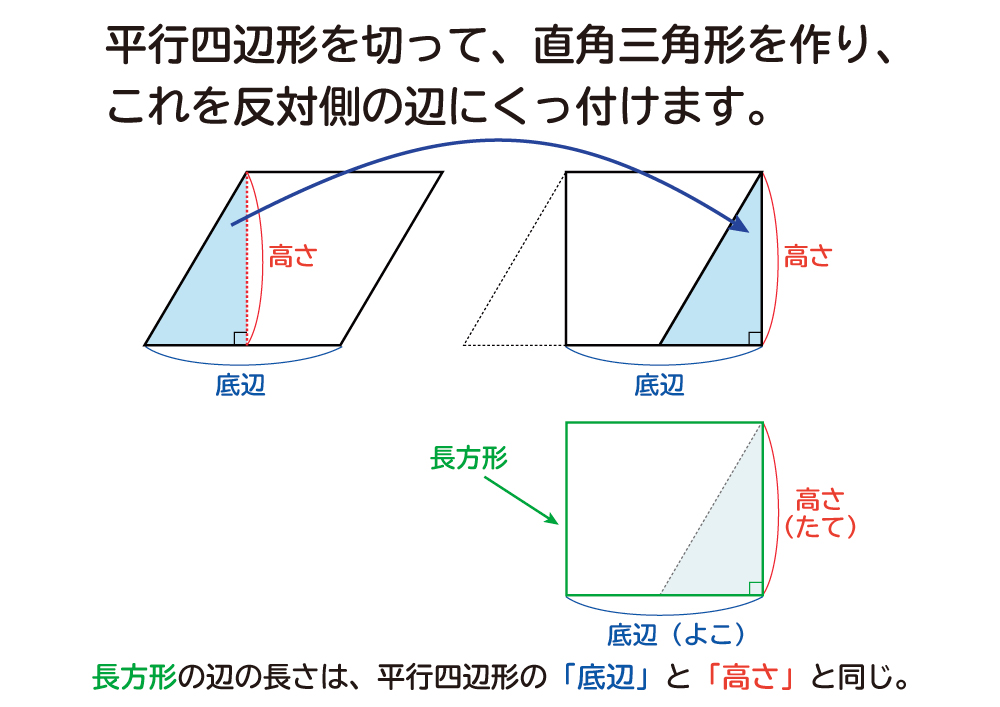
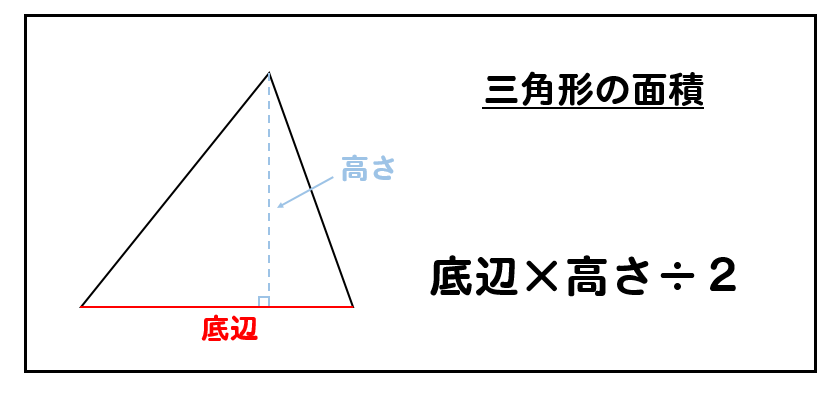
(底辺)×(高さ)÷2 で求められます。 次のように分数の形で書くこともできます。 (面積)= (1) 2で割ることを忘れる答案が多いので注意しましょう。 右図2の三角形の面積は、 4 × 3=12 ではなく、 4 × 3 ÷ 2=6 になります。 (2) 高さは必ず底辺に垂直(直角)な線で測らなければなりません平行な2本の対辺を台形の底辺 と 用語で表現するなら(上底 下底)×(高さ)÷ 2 である。この公式は、台形を対角線で2つに分けたときの各々の三角形の面積が ah/2 および bh/2 であることから得られる。この公式を導く別の方法としては、まず2つの台形を上底と下底以外の辺(上図での AD 三角形の面積は、(底辺) × (高さ) の 長方形 の 半分 だから (底辺) × (高さ) ÷ 2

Page 2 2 円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチニュース
底辺×高さ÷2 なぜ
底辺×高さ÷2 なぜ- なぜ底辺と高さが同じなら全ての三角形の面積は等しいのか 三角形の等積変形は底辺と高さが同じであることを利用して面積を変えずに三角形の形を変えることができるが、そもそも底辺×高さ÷2という式はどこから出てきたのだ? 三角形の2つの辺それぞれに平行な直線を引いて平行四 なので、長方形の面積「縦 (高さ)×横 (底辺)」を2つに分ける「÷2」で三角形の面積なのです。 10人 がナイス!



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ
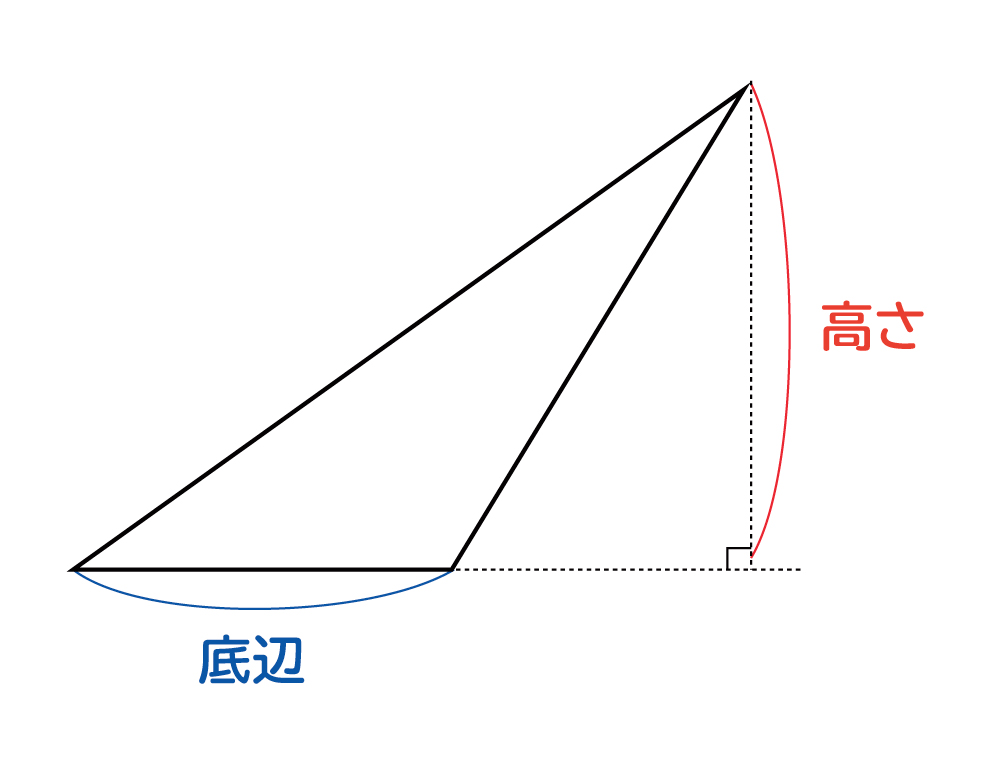
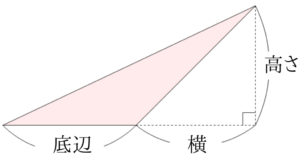
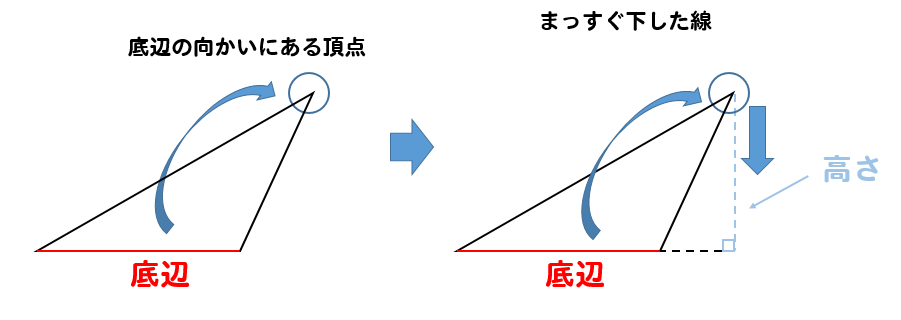
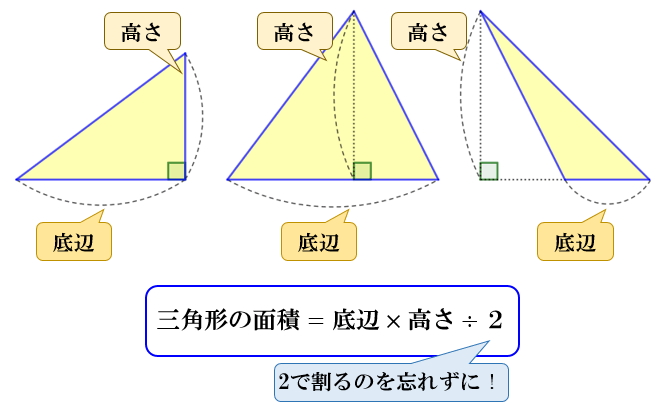
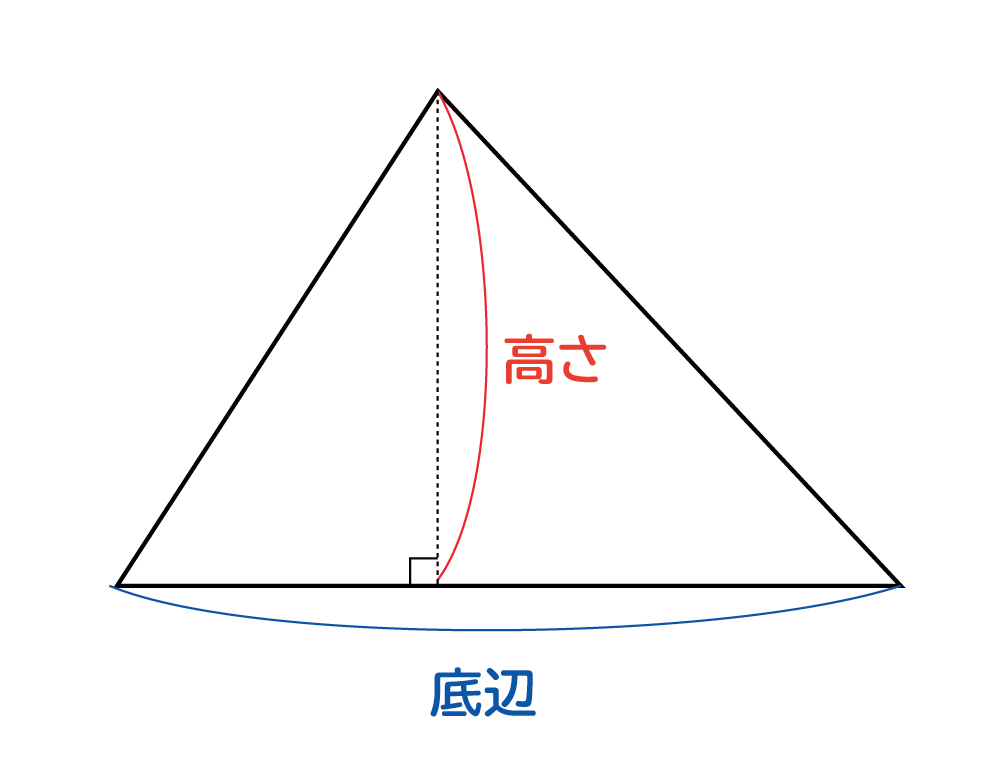
面積=底辺×高さ÷2 底辺とは、三角形の中で高さを測るための基準となる辺のことをいいます。高さとは、底辺が含まれていない頂点に対して底辺から直角に引いた線をいいます。 2正三角形 正三角形の面積の公式は、下記の通りです。 面積=(一辺)×(一辺)×043 正三角形とは、三 第1回 ガウス・ボンネの定理から底辺×高さ÷2の公式へ 数学, 物理, ピタゴラスの定理, 相対性理論 この記事を読むのに必要な時間:およそ 1 分 本書 (ピタゴラスの定理でわかる相対性理論) p 6566では, 球面三角形の面積について解説を行ったのですが考える数学、技術 次ぎの考える数学問題を解きなさい。 1 + 1 = 1 ー 1 = 1 × 1 = 1 ÷ 1 = 0.1 + 0.1 = 0.1 ー 0.1 = 0.1 × 0.1 =
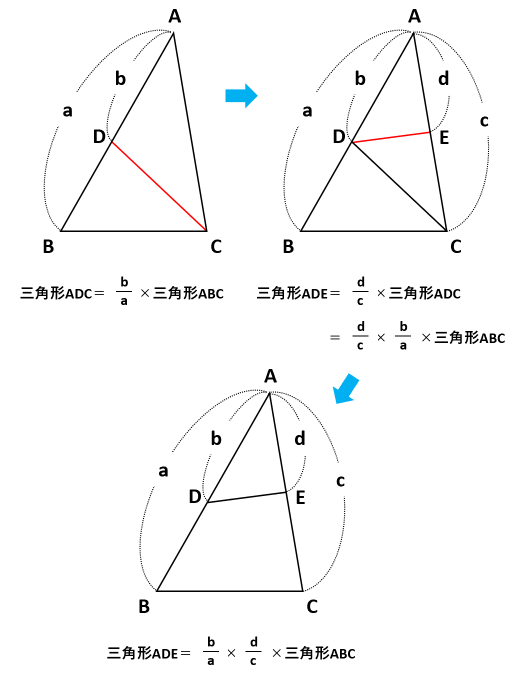
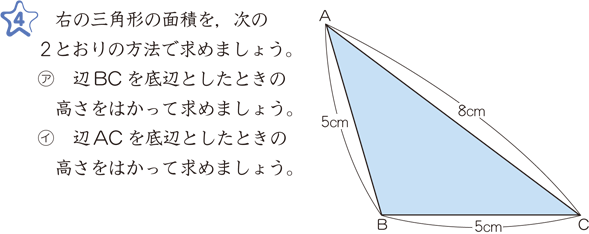
三角形だと底辺×高さ÷2なのに、台形だと上底+下底ってなるのか。 何年の学習指導要領で小中学校を過ごしてきたのだろう。 一時期台形の面積がなかった時期があったと記憶している。 台形を対角線で切り離す。面積は2つの 三角形の和だ。 (上底下底)×高さ÷2 = 上底×高さ÷2+下底×高 三角形の面積は底(底辺の長さ)×高さを2で割るので、2が出てくる。 ということは、 底(平面図形では長さ、立体図形では面積)×高さを次元数で割れば良さそうであることは、 すぐに見当がつくであろう。 ということで、n次元の錐体の場合は、nで割れば良い。 これは、n次元立方体を(面積)=(底辺)×(高さ)÷2 の公式で求められるので, (面積)と(底辺)の長さが決まっていたら,(高さ)が求まる (解答) abc の面積は ebd の面積は abc の面積を二等分しているのだから (答) 例4 3点 a(2, 4), b(0, 0), c(6, 0) を頂点とする abc がある. 線分 bc 上の点 d(4, 0) を通
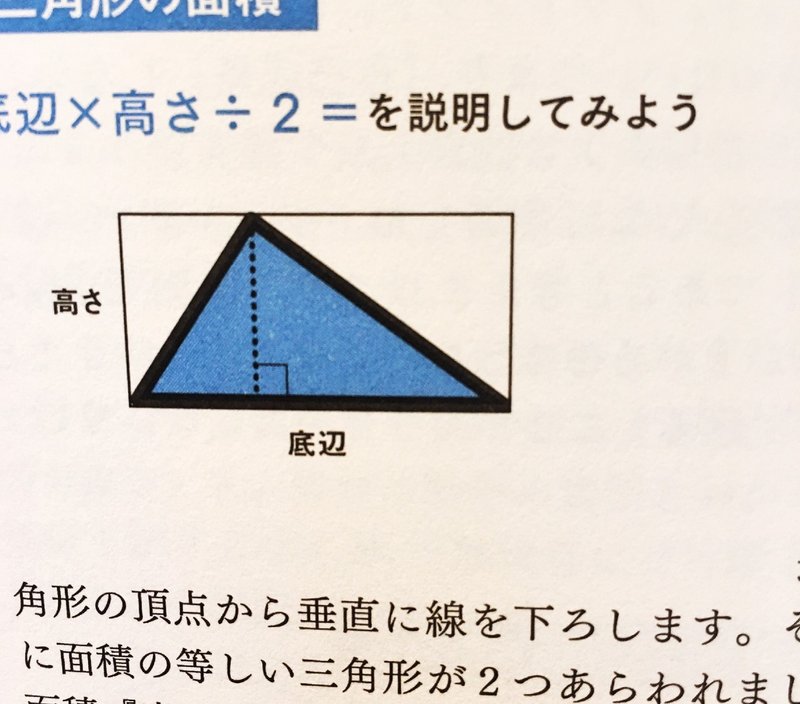
長方形の面積が (底辺)× (高さ)であることは既知とします。 長方形の対角線を引くことにより、直角三角形の面積が (底辺)× (高さ)÷2になることは明らかです。 三角形の面積は 底辺×高さ÷2 で求める。 それだけをポンと渡されてなぜそうなるのかを知らないから、全然覚えられないし、応用ができなくてとても困っていました。 最近読んだ本でそのなぜを知ることになり衝撃を受けたのですが まず、三角形を含む長方形を書きます。三角その時の高さはもう一方の対角線の長さの半分になっています。 対角線①⇒底辺 対角線② ÷2 ÷ 2 ⇒高さ 平行四辺形の面積は『底辺×高さ』なので、元のひし形の 『対角線×対角線÷2 ÷ 2 』 がひし形の面積になるのです。 ちなみに平行四辺形の面積が『底辺×高さ』になる理由はこちらにまとめています。 平行四辺形の面積の公式|なぜ『底辺×高さ』で求め




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
底辺 × 高さ ÷2+ 底辺 × 高 さ ÷2+ 底辺 × 高さ ÷2+ 底辺 × 高さ ÷2+ 底辺 × 高さ ÷2+ 底辺 × 高さ ÷2+ 底辺 × 高さ ÷2+ 底辺 × 高さ ÷2 がピザの面積である。しかし計算が面倒なので、底辺の長さをすべて足してから、"× 高さ ÷2"をする。計算式にすると次のようになる。これは上の式 この公式は非常に美しいですが,必ずしも覚える必要はありません (もちろん覚えてしまってもよいですが)なぜなら,三角形の $3$ 辺が与えられれば,余弦定理よりひとつの角の余弦がわかります.そこから正弦を求めて,公式 $ S=\frac{1}{2}ab \sin \theta$ を用いれば,三角形の面積が 0 件 質問者: zuku79 質問日時: 0737 回答数: 6 件 平行四辺形の面積の公式では底辺×高さ、三角形では底辺×高さ÷2なのに、なぜ長方形は、底辺や高さという言葉を使わずたて×よこなのでしょうか。 また、なぜたてが初めにきて横ではないのでしょうか。 通報する この質問への回答は締め切られました。



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




平行四辺形の面積の求め方 公式と計算例
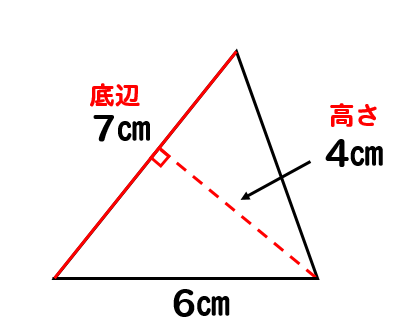
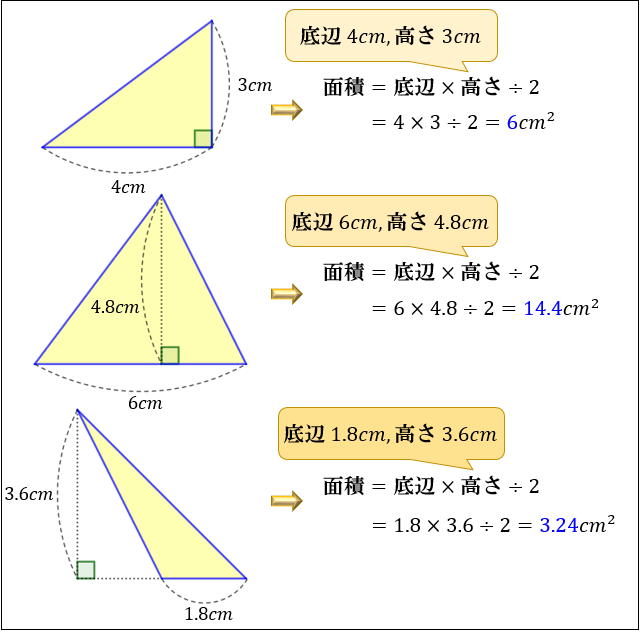
先生「三角形の面積は底辺×高さ÷2で導けます」人間達「はーい! 」ワイ「なんでや」 学校 学校の制服いらなくね? 18年4月4日 学校 なんで不登校って学校来れない 底辺 × 高さ ÷ 2 で計算することができます。 円の面積は「半径」の1つだけがわかれば答えが出ましたが、 三角形は「底辺」と「高さ」の2つが必要になります。 ここで必要になるのが「変数」というものです。 変数とは?? 変数とは数字の入れ物です。三角形の面積の公式はどうして底辺×高さ÷2なのか? 三角形の面積は底辺 × 高さ ÷ 2で求めます。 底辺が 6cm、高さが 4cm の三角形は 6 × 4 ÷ 2 = 12cm 2 になります。




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



面積の考え方 算数の教え上手 学びの場 Com
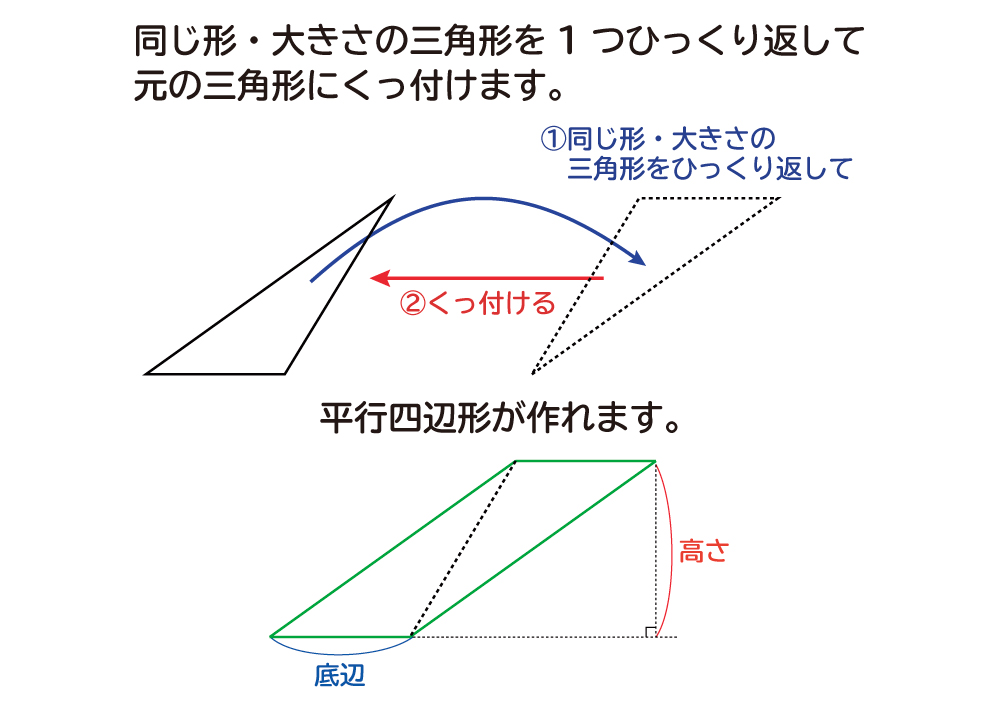
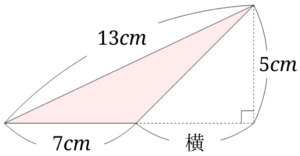
求める鈍角三角形の面積は、図の赤い長方形の面積と等しいことが分かります。 赤い長方形の縦の長さは高さ÷2、横の長さは底辺なので、鈍角三角形の面積は底辺×高さ÷2ということが分かります。 鈍角三角形の面積はなぜ底辺×高さ÷2 part2 三角形の面積の公式は、「底辺×高さ÷2」です。 「なんで2で割るの?」と聞かれたら、答えは簡単。 「この三角形と同じ三角形を上下ひっくり返してくっつけてごらん。 平行四辺形になったでしょ。この平行四辺 底辺×高さ÷2=(1/3×1/3×√3/2)÷2=√3/24 (2) 正四角形の場合 1辺の長さは1/4であることから、その面積は、 1/4×1/4=1/16 (3) 正六角形の場合 1辺の長さは1/6であり、p2の図で示したように6つの正三角形に分割できることから、その面積は、



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校



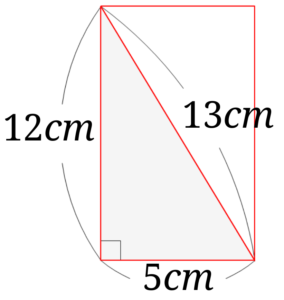
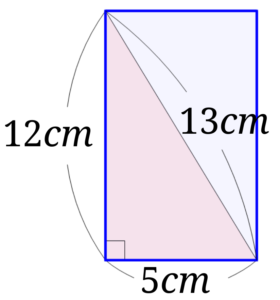
斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
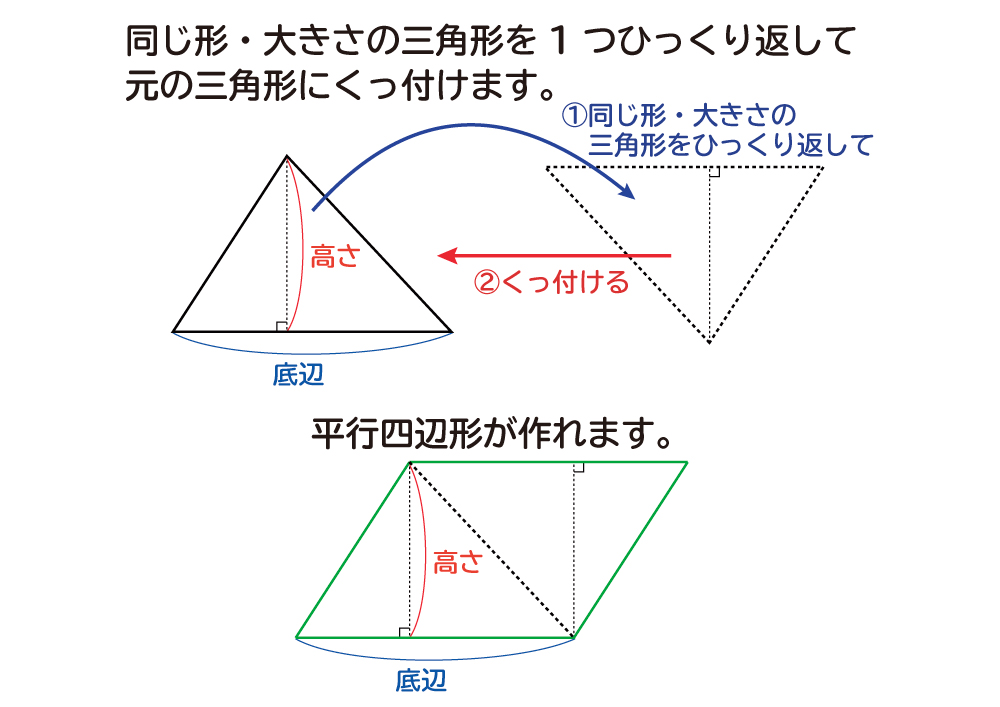
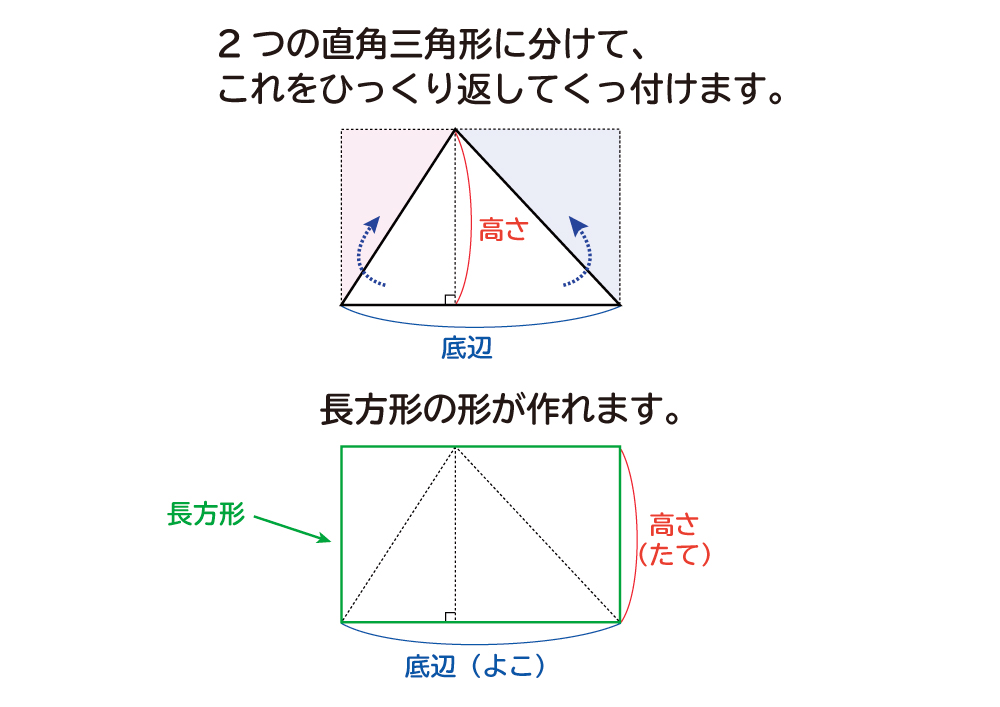
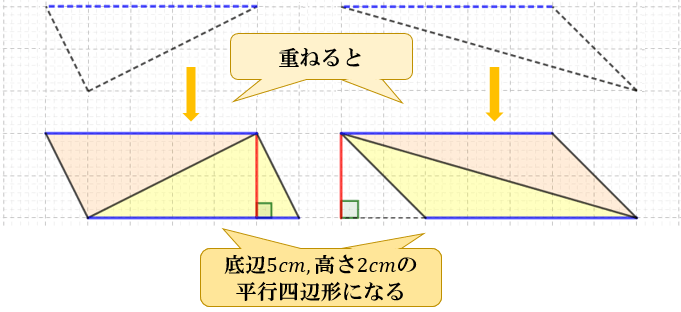
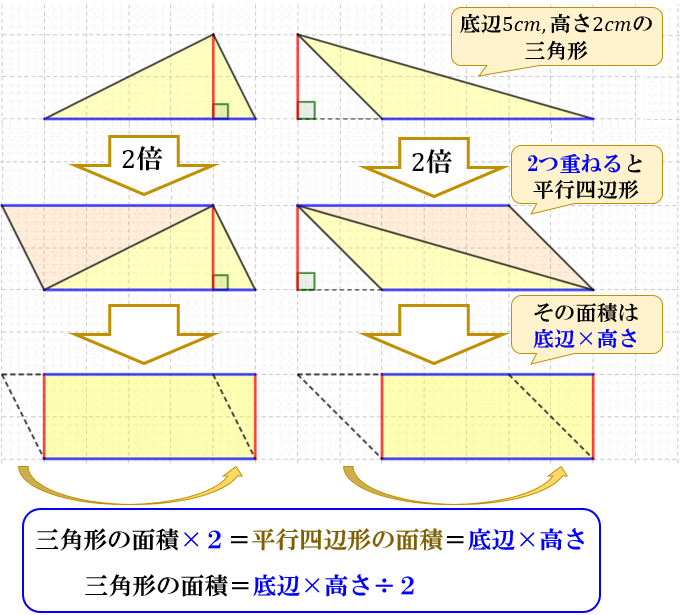
三角形の面積の公式は、「底辺×高さ÷2」です。 「なんで2で割るの?」と聞かれたら、答えは簡単。 「この三角形と同じ三角形を上下ひっくり返してくっつけてごらん。 平行四辺形になったでしょ。この平行四辺形の面積を2で割ればいいんだよ。」 では、円錐・角錐などの錐体の体積は「底面積×高さ÷3」ですが、 なぜ3で割るのでしょうか? 私が昔中学生の頃三角形の面積は底辺×高さ÷2です。 やはり相似比が1:nに対して、面積比が1n^2です。以上より、相似比と面積比の関係は下記となります。 相似比がmnのとき面積比は まとめ 今回は相似比について説明しました。意味が理解頂けたと思います。相似比は、相似な図形における辺の長さの比率 先生「四角形は三角形2つなので四角形の面積を求めて2で割ればいいから、底辺×高さ÷2で導けます」 人間達「はーい!」 イッチ「なんでや」 先生「では次の問題へ進みます」 人間達「はーい!」 ワイ「なんで2で割るんや」 先生「ぺちゃくちゃ」
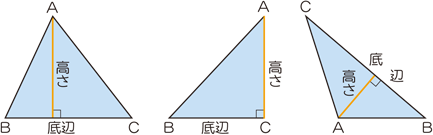



底辺と高さ 算数用語集



なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋
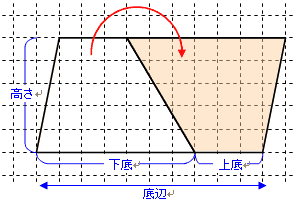
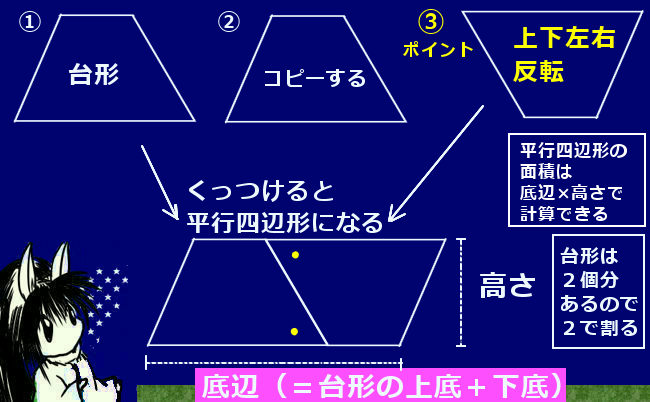
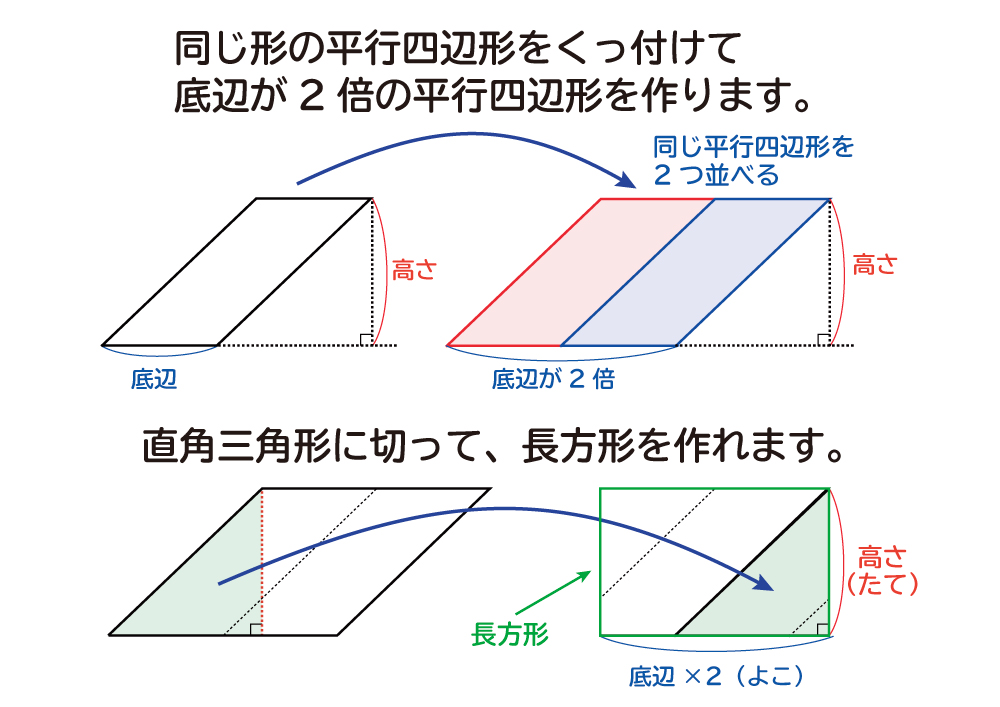
この平行四辺形の底辺の長さは、元の台形の(上底+下底)と同じ長さになっています。 この平行四辺形の面積は「底辺×高さ」=「(上底+下底)×高さ」 で求めることができます。 そのため、 台形の面積は平行四辺形の面積の半分なので「(上底+下底)×高さ÷2」 で求めることができます。 台形を2つくっ付けて、平行四辺形を作ることができたね! ・ 同じ底辺×高さ÷2=三角形の面積 8㎠ くふう! 長方形に形を変えて求めた。 底辺 くふう! 5cm 高さ 4cm 平行 へいこう 四辺形 し へんけい の面積 三角形 底辺 ていへん ×高さ たか ていへん 底辺 底辺×高さ=平行四辺形の面積 A ㎠ 名 前 さんかっけい の面積 ×高さ たか 高さ 4cm 底辺 4cm 同じ大きさ




底辺と角度から 高さを求める ある高さの木から 10m離れて 木の 数学 教えて Goo




この問題の解説にひいてある青線のところがなぜそうなるのかわかりません Clear
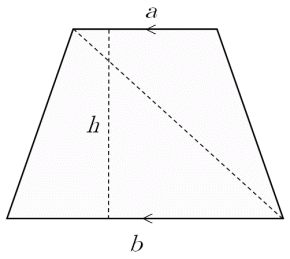



初等幾何 台形の面積はなぜ 上底 下底 高さ 2 なのか 大人が学び直す数学
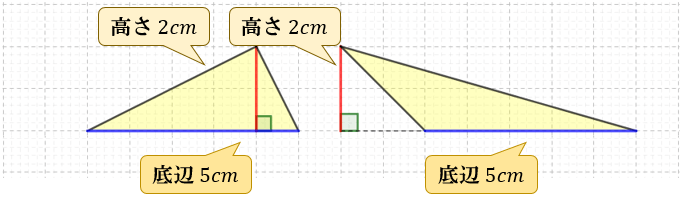



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
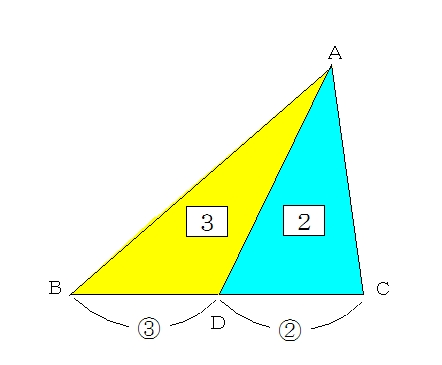



辺の比と面積比




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



底辺と高さの等しい三角形の面積が等しいのはなぜですか 同じ三 Yahoo 知恵袋




ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル
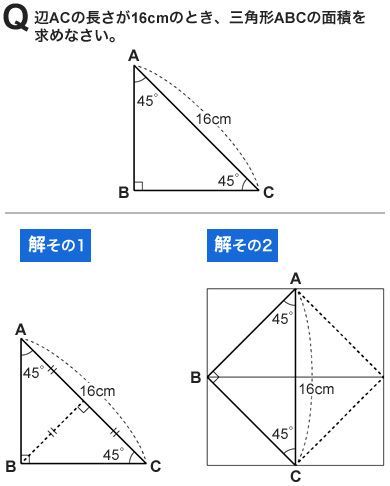



256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




これの答えって2乗しないんですか なぜ9 64ではいけないのでしょうか Clear




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




高さがわからない台形の面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




平行四辺形の面積の求め方 公式と計算例
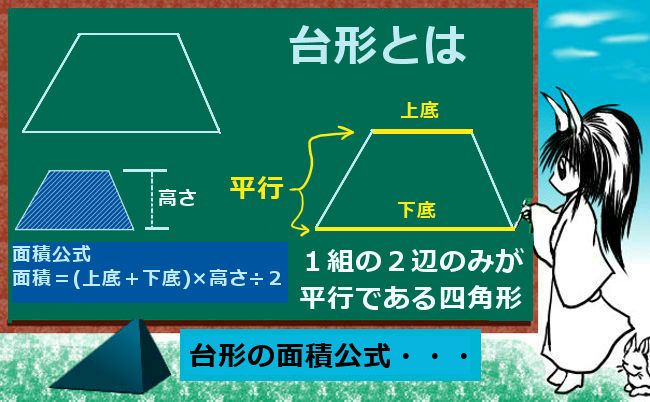



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




Page 2 2 円の面積はなぜ 半径 半径 3 14 仕組み がわかれば算数は面白い ダ ヴィンチニュース




三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
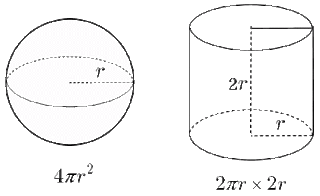



初等幾何 三角形の面積はなぜ 底辺 高さ 2 なのか 大人が学び直す数学
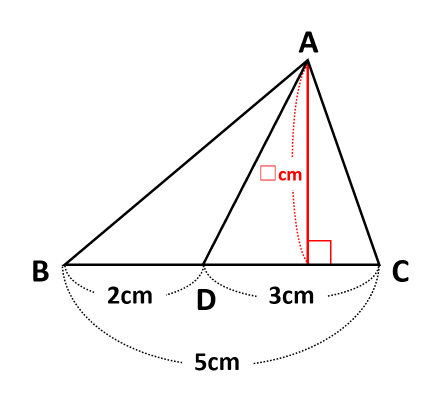



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ




なぜ底辺と高さが同じなら全ての三角形の面積は等しいのか 数学が嫌いなんです
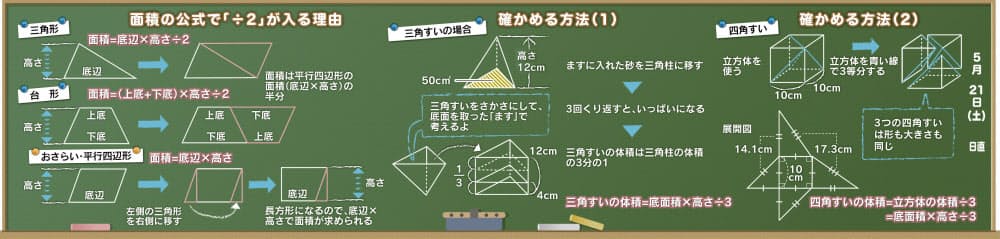



円すいの体積確かめよう なぜ円柱の3分の1 Nikkei Style



3



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校




三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



今週の1題



台形の面積公式 算数と図形 理数系無料オンライン学習 Kori



3



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



Tan45度の値は 1分でわかる意味 値 Cos45度 Sin45度との関係




三角形の面積って 底辺 高さ 2 ではありませんでしたか それとも今回 数学 教えて Goo



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



三角形の面積はなぜ底辺 高さ 2なの 鋭角三角形 直角三角形 鈍角三角形のそれぞれについて解説します みけねこ小学校
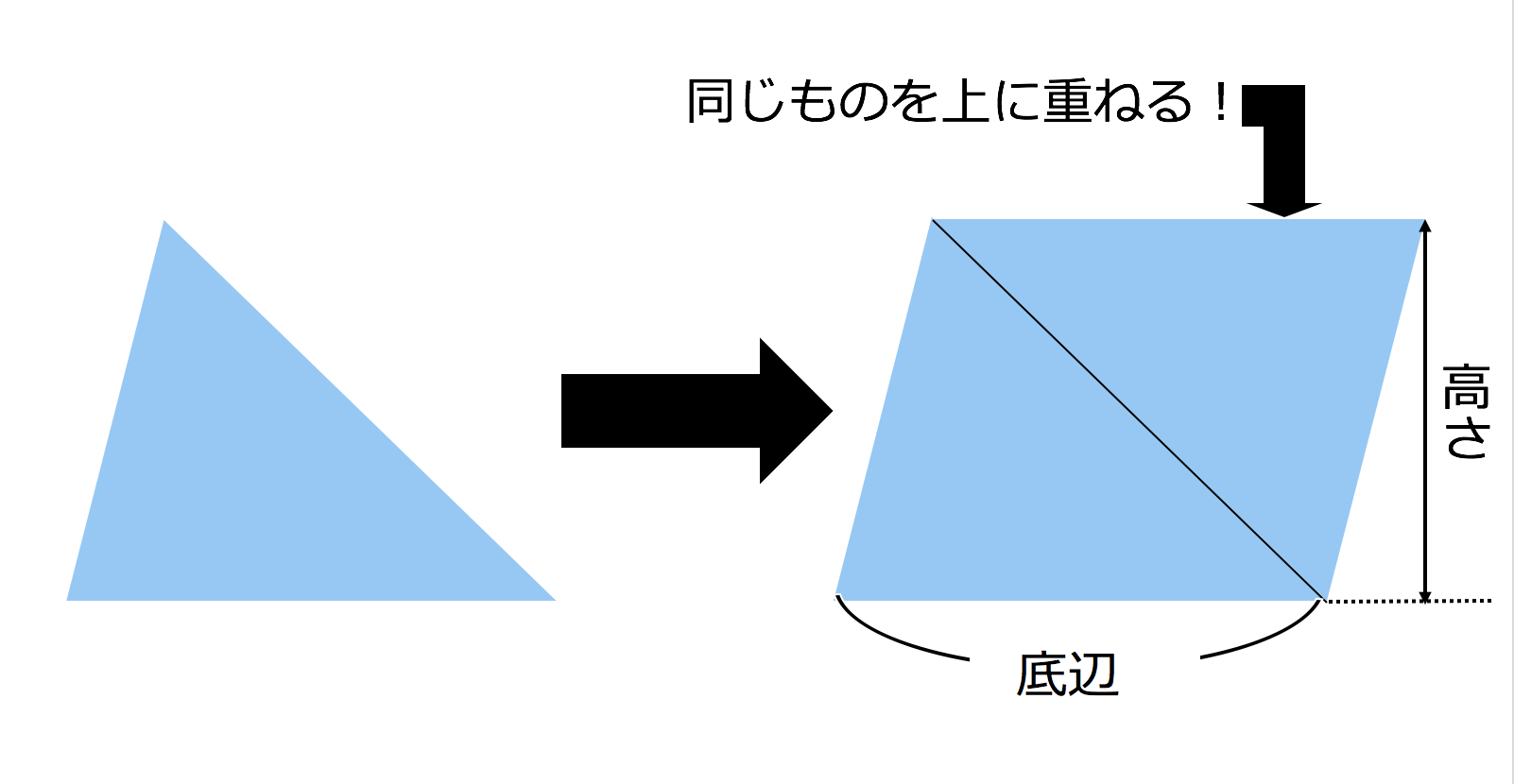



3分で分かる 正三角形の面積の求め方 公式をわかりやすく 合格サプリ
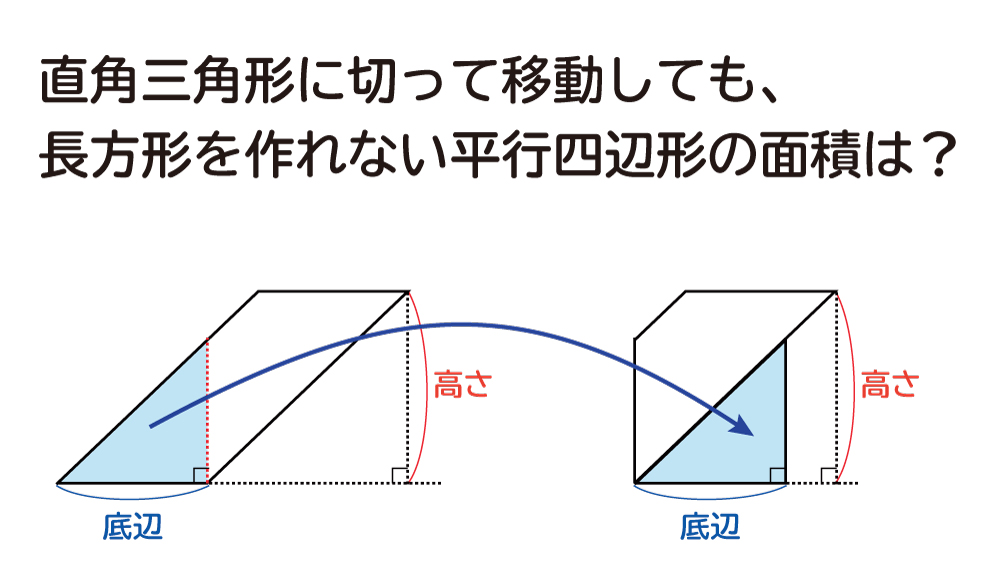



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




三角形の面積の公式 2 って どうして2で割るの



3
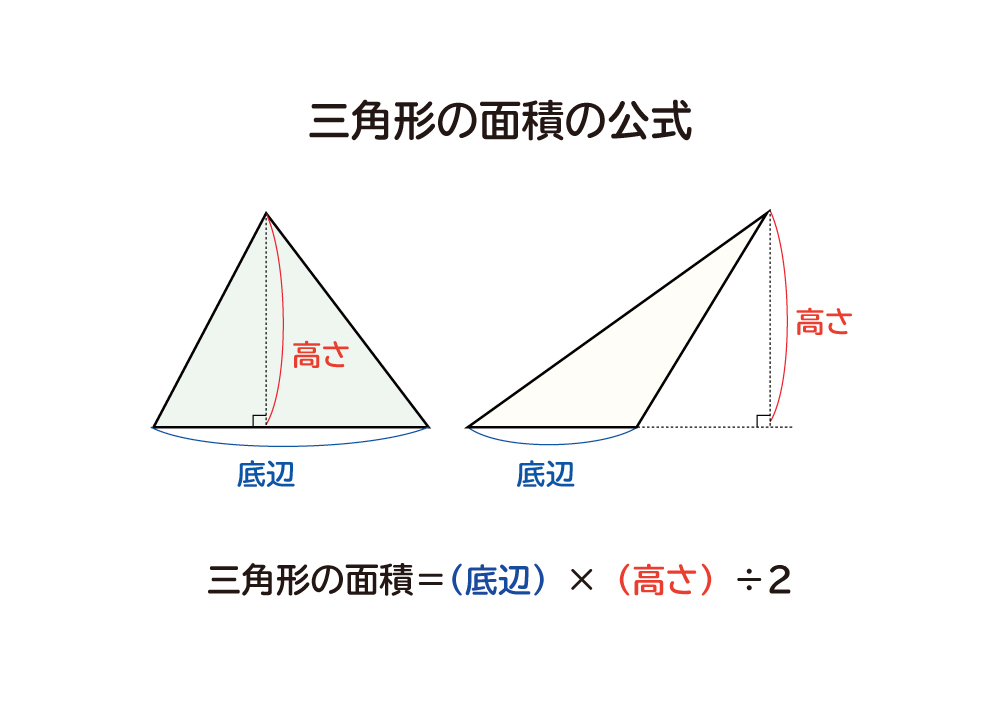



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



なぜ三角形は底辺 高さ 2なのですか どうして 2がはいるのです Yahoo 知恵袋




三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



三角比の定義は 1分でわかる定義 覚え方 表 直角三角形と単位円との関係
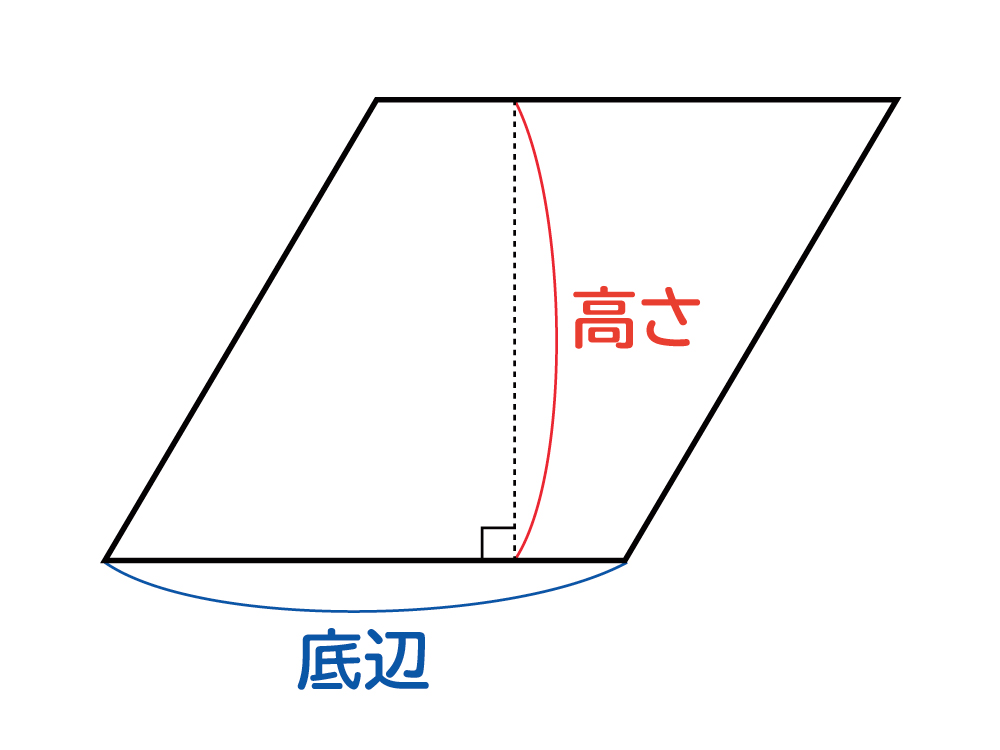



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
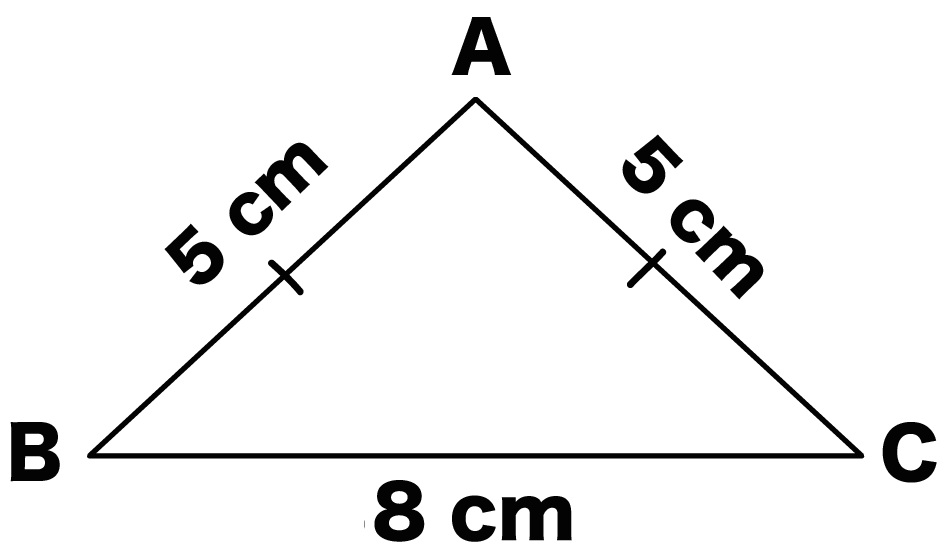



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
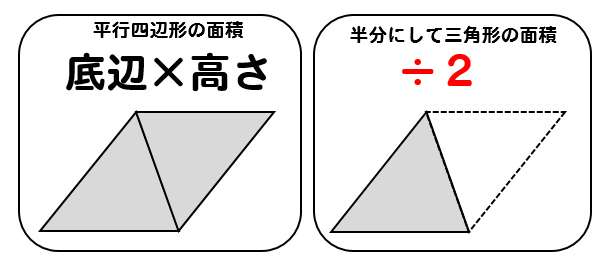



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ




台形の面積の公式 小学生に教えるための分かりやすい解説 数学fun




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun
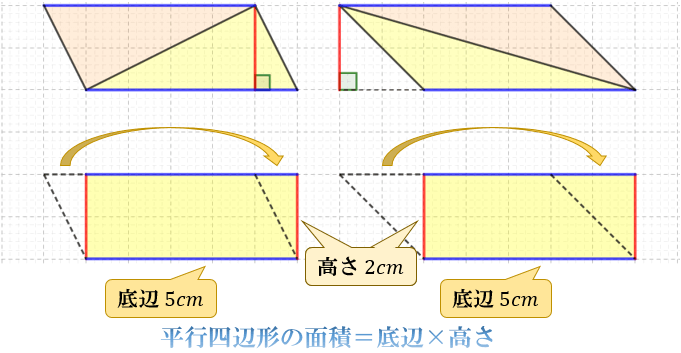



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



図形の扉 面積のひみつ




なぜsinなのですか Clear




平面図形が苦手な人は必見 三角形の面積比と辺の比の関係 基礎編



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun




数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



底辺 高さ 2 のストーリー Chie Oikawa Coach Barista Cook Note



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める



数学 正三角形の高さと面積は5秒で出せる 受験の秒殺テク 4 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



底辺と高さ 算数用語集




直感的に求めよう 直角三角形の面積の求め方 パパが教える算数教室



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典
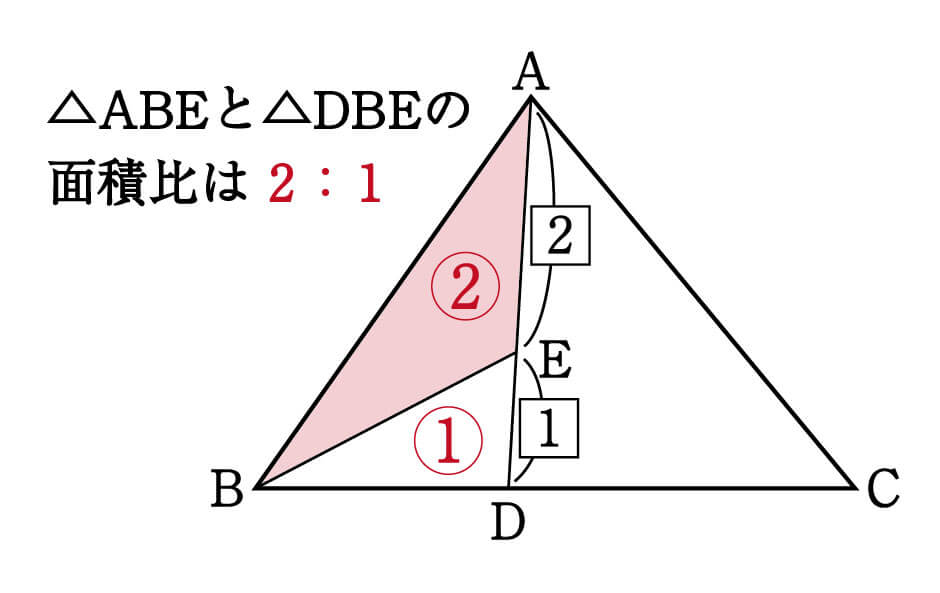



数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




が分かりません Adm解き方 Dbmの比が4 3になるのは分かるのですが なぜ二 Clear



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




1 はa 18 b でもいいんですか Clear




平行四辺形の面積の公式 なぜ 底辺 高さ で求められるのか 数学fun



なぜ 三角形の面積は 底辺 高さ 2 なのか を説明します おかわりドリル



なぜ三角形の高さがb Dになったのですか また この面積比になる仕組 Yahoo 知恵袋



なぜ 平行四辺形の面積は 底辺 高さ なのか を説明します おかわりドリル




平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



二等辺三角形の角度は 1分でわかる求め方 計算 辺の長さとの関係 証明
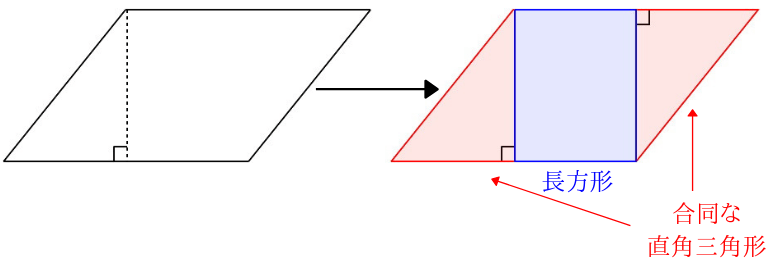



平行四辺形の面積の求め方で習う公式は なぜ底辺 高さになるの みけねこ小学校



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




三角形の面積の公式 2 って どうして2で割るの



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学
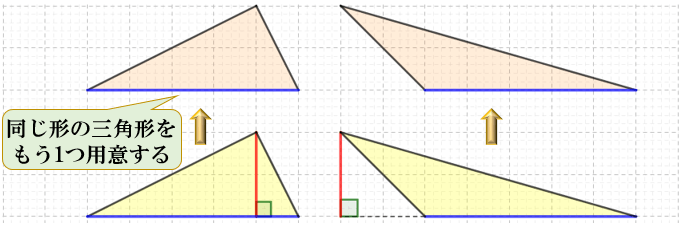



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ
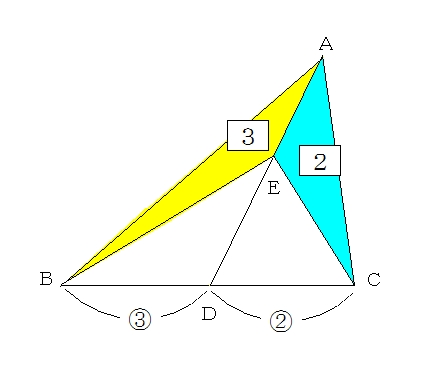



辺の比と面積比
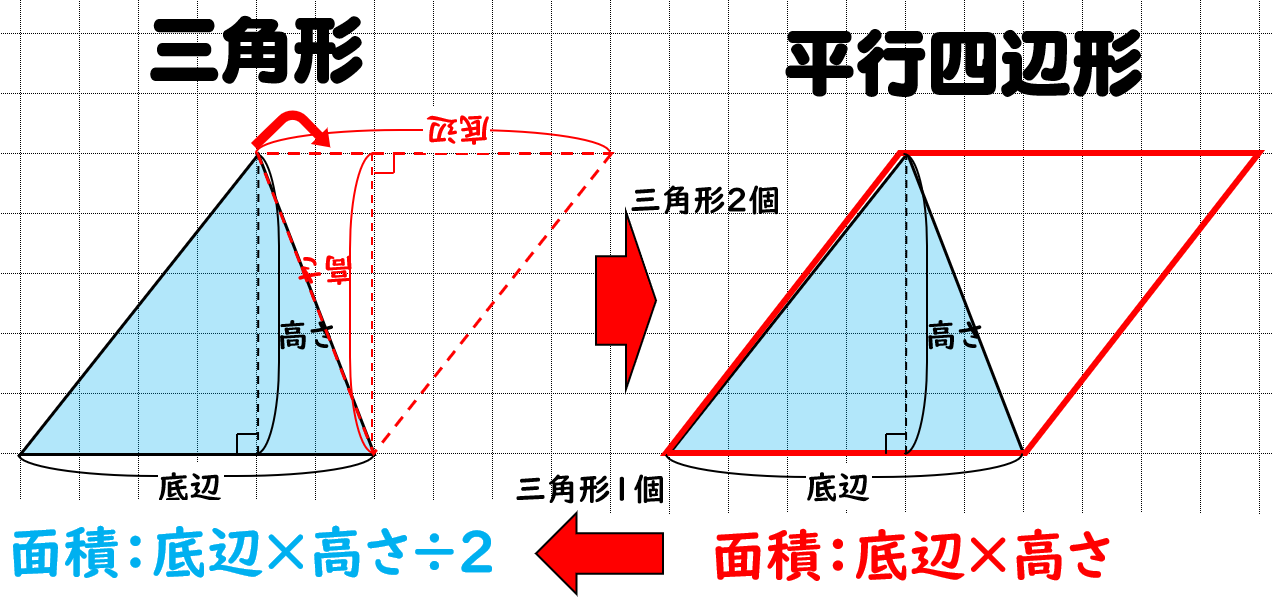



三角形の面積の公式 小学生に教えるための分かりやすい解説 数学fun



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




平行四辺形の面積は 底辺 高さ かけ算の順序の昔話




面積の求め方 計算公式一覧




三角形の面積を求める方法は何通り その1 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
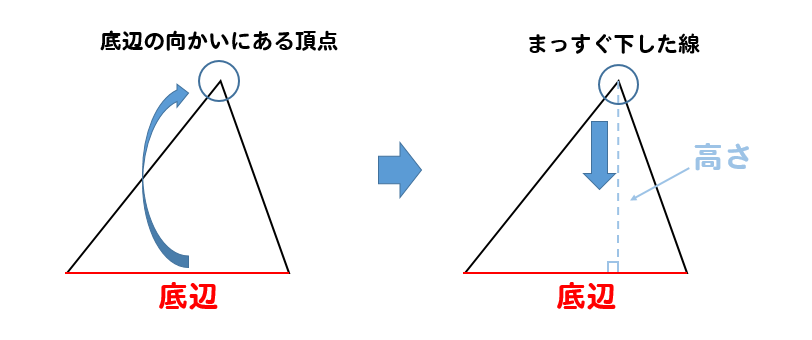



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



三角形の面積公式 小学生はどうやって解く 問題を使って解説 数スタ



同じ長さの長方形と平行四辺形ではどうして面積が違ってくるのでしょうか 例え Yahoo 知恵袋



三角形の面積の求め方 なぜ底辺 高さ 2で求まるのか アタリマエ




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



0 件のコメント:
コメントを投稿