前記キャピラリー・チューブ(2)は、底角αが48度と60度の間の値を採る 二等辺三角形 の形状をしており、前記反射表面(4)は、前記キャピラリー・チューブ(2)の 二等辺三角形 の一方の側面に対向して配置される。三角形の合同条件を利用して二等辺三角形の性質と条件等を学習した後に,その利用の1つと して位置づけられることが多いであろう。 この場合 ,そ れを定理としてまとめるにあたって合同条件を示すのに二等辺三角形の性質を用いたいからです。 三辺相等の合同の定理は 他の合同条件にくらべて やっかいなのです。 さて、これで 「二辺挟角」「二角挟辺」「三辺相等」という 2つの三角形が合同になるための 3つの定理が出そろいました。
直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
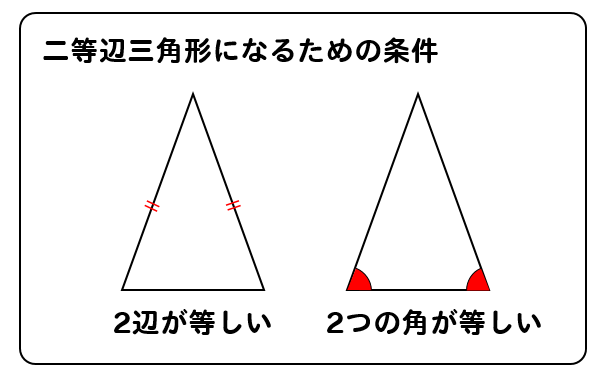
二等辺三角形の条件 小学三年生
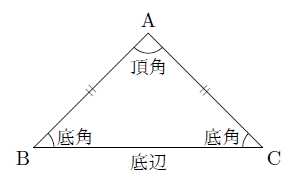
二等辺三角形の条件 小学三年生-動画で学習 2 二等辺三角形になるための条件 数学 もう一度見る Play Video Play Mute Current Time 000 / Duration Time 000 Loaded 0%2 つの辺が等しい三角形を二等辺三角形という(定義 ていぎ)。 右図のようなab=ac の二等辺三角形で, ∠aを 頂角 ちょうかく ,頂角に対する辺bcを底辺 ていへん , 底辺の両端の∠bと∠cを 底 てい 角 かく という。 問題(後期期末)



1
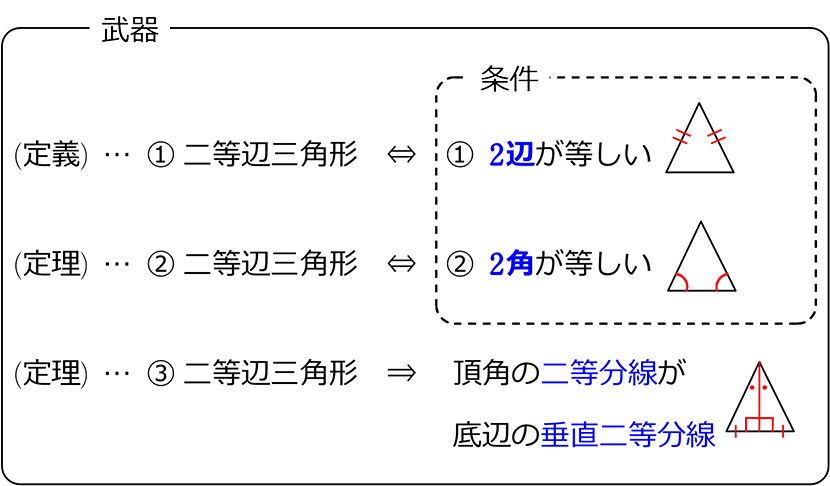
T:「『 二等辺三角形になるための条件』といいます. 三角形が二等辺三角形とまだわかっていない ときに使うので『2つの角』と表現します.」 ・黒板の図で生徒に簡潔に説明させる. ・「二等辺三角形になるための条件」とし て黒板に整理する. 二等辺三角形とは?定義 二等辺三角形とは、 \(\bf{2}\) つの辺の長さが等しい三角形 のことです。 二等辺三角形の等しい \(2\) 辺の間の角のことを「頂角」、その他の \(2\) つの角のことを「底角」といいます。そして、頂角に向かい合う辺のことを「底辺」といいます。三角形の成立条件(存在条件):三辺の長さが a, b, c a,\b,\c a, b, c である三角形が存在する必要十分条件は, a b > c ab > c a b > c かつ b c > a bc > a b c > a かつ c a > b ca > b c a > b
三角形の成立条件 および 直角三角形,鋭角三角形,鈍角三角形であるための条件 1 三角形の成立条件 abc において,辺bc,ca,ab をそれぞれ\a;\c をそれぞれ辺bc, ca,ab の対角という. 以下では, abc の\a;二等辺三角形の底角が等しいという性質を利用する △DBCはDB=DCの二等辺三角形なので∠DCB=∠DBC=25° 三角形の外角はそれと隣り合わない2つの内角の和に等しいので∠ADB=50° △ABDはAD=ABの二等辺三角形なので∠ADB=∠ABD=50°
続いて y y は、二等辺三角形 ABC A B C の底角が 66° 66 ° であることから、 ∠y = 180−66× 2 = 48° ∠ y = 180 − 66 × 2 = 48 ° と求まります。 水色の三角形と三角形 ABC A B C は、 3 3 つの角がそれぞれ同じ大きさなんですね! ※ちなみにこれを「相似」といいます。 二等辺三角形の定義、定理、基本的な証明問題の練習プリントです。定期テストにもよく出題されますので、確実に出来るようにしましょう。 二等辺三角形の定義「二つの辺の長さが等しい三角形」 等しい二辺の間の角を頂角という。 頂角に向い合う辺を底辺という。二等辺三角形になるための条件(定理) 二つの角が等しい三角形は、それらの角を底角とする二等辺三角形である。 この条件は(定理)でもあるから、もちろん二等辺三 角形の定義から証明して導くことができるんだ。




ม 2 โน ตของ 二等辺三角形の性質 ช น Junior High数学 Clear



1
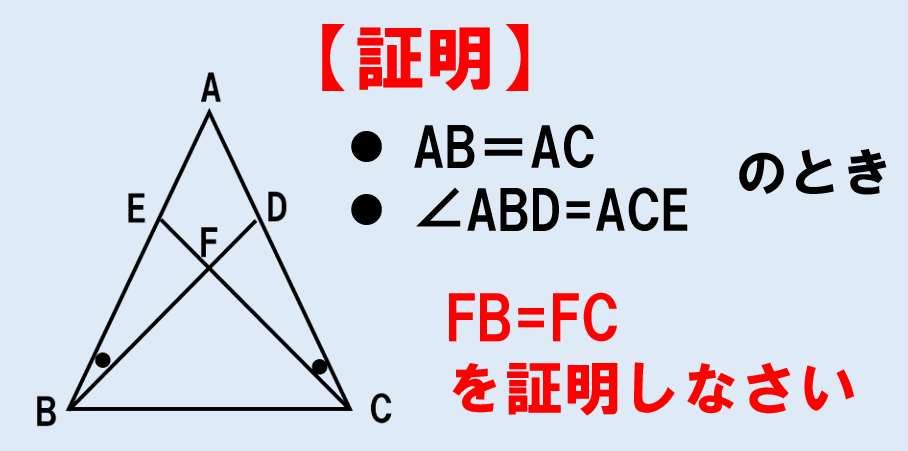
二等辺三角形ではない三角形を思い浮かべてください。 いろんな三角形が思い浮かんだと思いますが、その中に正三角形はありましたか? ないですよね? すなわち 二等辺三角形ではない ならば 正三角形ではない これは今、想像してもらった通り真です。二等辺三角形2 2 2 右の図で abcはab=acの二等辺三角形で、bd=ceである。また、cdとbeの交点をfとするとき fbcは二等辺三角形になることを証明しなさい。直角二等辺三角形となるための条件は,実数(大きさ)を用いて α=β (*1) α 2 β 2 =β−α 2 (*2) のように連立方程式で書いてもよいはずです.(問題の形によってはこの形の方が使いやすい場合もある) (*1)(*2)と(2)とは次のようにつながる.




定理 二等辺三角形の両底角は等しい を使って 身勝手な主張



外接円 外心について
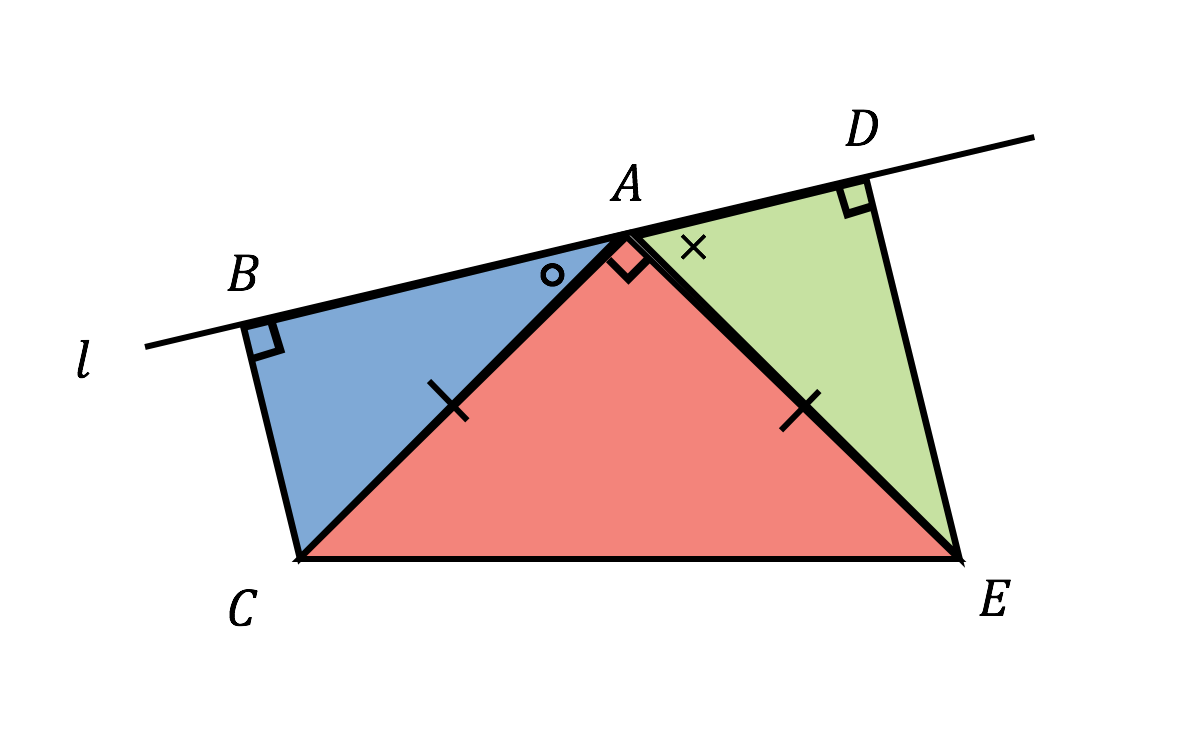
次に, 三角形の合同条件(3 辺相等) が成り 立てば,2 つの三角形は合同であることの証明 について述べる。この証明は, 二等辺三角形 の底角定理を使って以下のように証明するこ とができる。 (証明) abc と dce において,ab=de, bc=ef, ca=fd ならば abc ≡ def三角形の合同条件を使い、「二等辺三角形の底角は等しい」ことを証明しよう。 まとめ どのような二等辺三角形であっても、底角は等しいといえる。 <説明するときのポイント> ①「 だからab=ac」というように 根拠を示すこと。 「2辺が等しい」(これが二等辺三角形の定義) または「2つの角が等しい」 が条件ですが、このほかに以下の2つのどちらかがいえても二等辺三角形になります。 1つ目



中学数学 図形の合同 図形の性質




ae Descubre Como Resolverlo En Qanda
二等辺三角形の合同条件を教えてください!! 二等辺三角形の定義 二辺の長さが等しい三角形 二等辺三角形の性質 ①二等辺三角形の2つの底角は等しい。 ②二等辺三角形の頂角の二等直角二等辺三角形の辺の比は「三平方の定理」から導くことができます。 直角二等辺三角形の底辺と高さの長さは同じです。 底辺(高さ)の長さを「1」として、三平方の定理に代入すると「斜辺 2 =底辺 2 高さ 2 ⇒ 斜辺 2 =11=2 ⇒ 斜辺=√2」になります。二等辺三角形 になるための 条件 二等辺三角形に なるための条件 を考察し,証明す ることができる。 ある定理の逆を いうことができ, それが成り立つ かどうかを調べ ることができる。 定理の逆の意味を 理解している。 二等辺三角形にな るための条件を理 解している。 3




二等辺三角形の証明の答えと解説お願いします Clear




この問題の一番大きい三角形と下の二等辺三角形同士で相似条件は満たせ その他 教育 科学 学問 教えて Goo
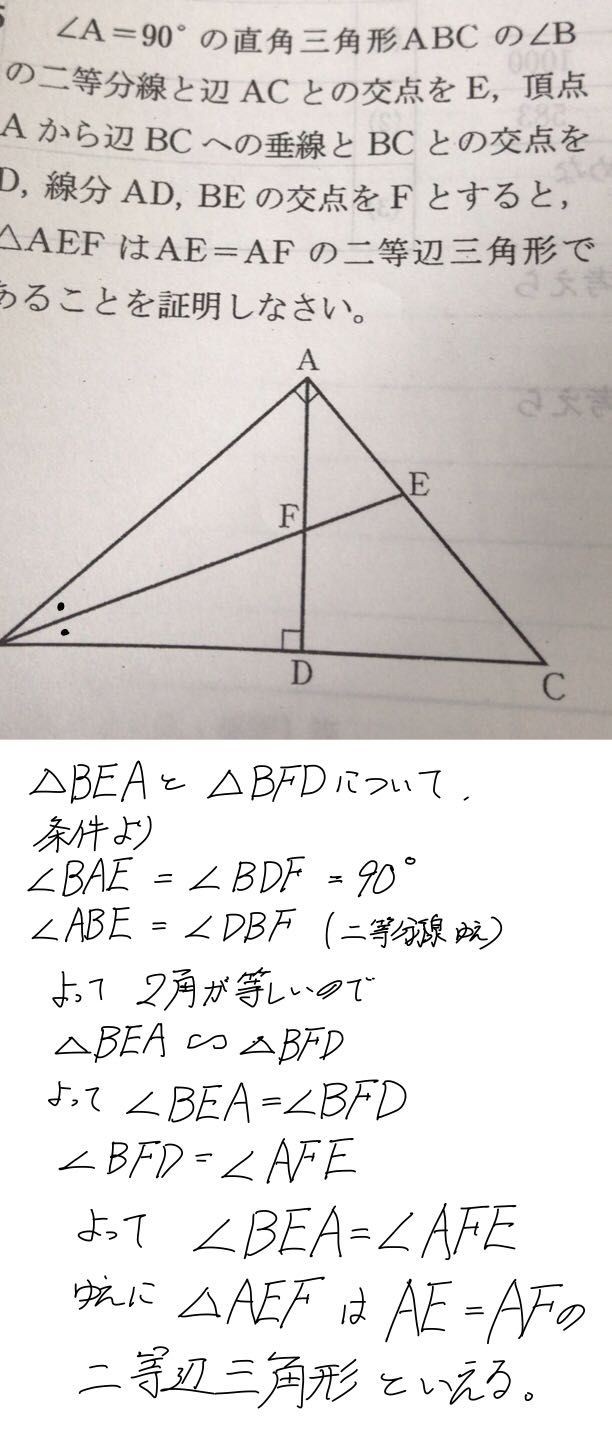
⑵ 二等辺三角形であることを証明する問題 問題文に示された条件 より,2点e,fを問題の図にかき入れると,次のよう になる。 2 三角形の内角と外角,二等辺三角形 ⑴ 三角形の内角と外角の関係を利用する。 ⑵ aefについて,∠aef=∠afeを示せば,二等 辺A b a c c b \b;二等辺三角形になるための条件を考察することができる。 定理の逆について理解することができる。 問題 右の図で, ABCは んな三角形だろうか? 4 B 二等辺三角形になるため の条件を見いだす活動。 逆について考え,反例を 用いて説明する活動。




簡単公式 直角二等辺三角形の面積の2つの求め方 Qikeru 学びを楽しくわかりやすく




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
間 ・ 二等辺三角形の2つの底角が等しいことを証明することができる。 ・ 定義、頂角、底辺、底角の意味を理解する。 教科書108、109ページの「とびらの問題」の名札立てをつくり、様々な三角形を見付け、それがどのような三角形であるかを示させる二等辺三角形になるための条件 解説 次の条件が成り立つとき,三角形は二等辺三角形になります。 三角形の2つの辺が等しい(定義) 三角形の2つの角が等しい 例題 無料動画講義(理論)二等辺三角形の合同条件 二等辺三角形の場合は、先ほど示した 一般的な三角形の合同条件を使う 必要があります。 ただし、 等しい 2 つの底角に対応する頂点は、どちらとどちらを対応させても構いません 。 直角三角形とは?




中2数学 二等辺三角形の性質2 頂角の二等分線 練習編 映像授業のtry It トライイット




3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
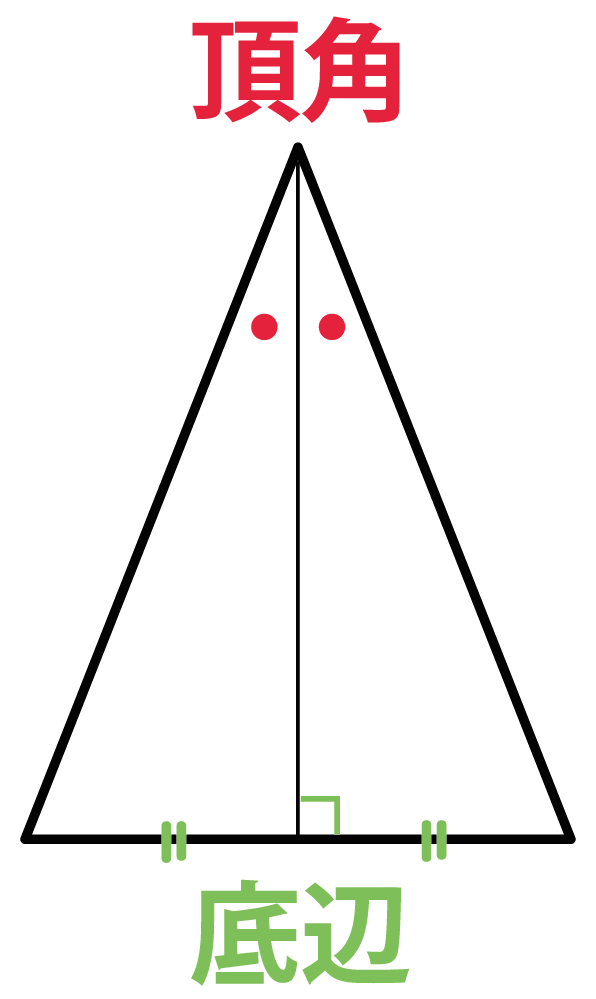
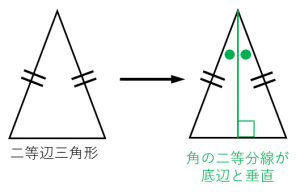
中津市立東中津中学校2年数学「三角形」二等辺三角形になる条件)河野秀男教諭 授業まるごと! 中津市立東中津中学校2年数学「三角形二等辺三角形と平行四辺形になるための条件について 教科書では二等辺 定理 二等辺三角形の頂角の二等分線は底辺を垂直に2等分する。 3つの角がそれぞれ等しいだけだと、「相似」とはいえても「合同」とは限りません。1 ア~カの中から,二等辺三角形を3つ選んで,記号をかきなさい。 ( ) ( ) ( ) 2 2~4について, 空欄をうめて,証明を完成させなさい。 2つの角が等しい三角形は,二等辺三角形である (二等辺三角形の 条件




直角二等辺三角形 Wikipedia




二等辺三角形と証明 Youtube
\(\triangle ABC\) が二等辺三角形であることを証明せよ三角形が二等辺三角形であることを示したいとき、・\(2\) つの辺が等しい・\(2\) つの角が等しいのどちらか片方がいえればOKです。これも暗記ですよ。三角形の合同条件を暗記したの同じように。AM= BM (仮 定) ∠PMA= ∠PMB=90°(仮定) 合同条件(2組の辺とその間の角) がそれぞれ等しいから, PAM≡ PBMで, PA=PB 4 二等辺三角形の等辺に,BD=CEとなる点D,Eをとるとき, PBCは二等辺三角形② 逆は「 ABC で,∠B=∠C ならば,AB=AC である。」である。2 つの角が等しい三角 形は二等辺三角形になるので,正しい。 ③ 逆は「2 つの直線 l, m に別の1 つの直線が交わるとき,同位角が等しいならば, l と m は 平行になる。」である。これは正しい。




世界一わかりやすい数学問題集中2 5章 図形の性質と証明



3分で分かる 直角二等辺三角形の定義 性質 証明などについてわかりやすく 合格サプリ
① 二等辺三角形の2つの底角は等しい。 ② 二等辺三角形の頂角の二等分線は底辺を垂直に二等分する。 ③ 二辺の長さが等しい三角形は二等辺三角形である。二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれぞれ




Laf先生に質問 Laf 中学生のオンライン学習塾 Facebook



3分でわかる 二等辺三角形の2つの定理 性質 Qikeru 学びを楽しくわかりやすく
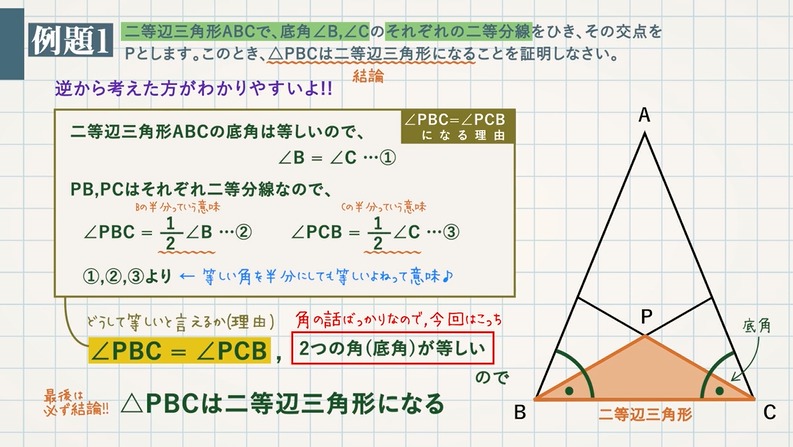



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
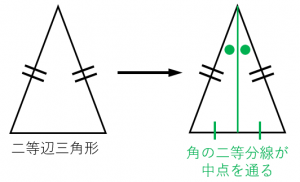



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ




二等辺三角形になることの証明 Youtube




二等辺三角形と証明 Youtube
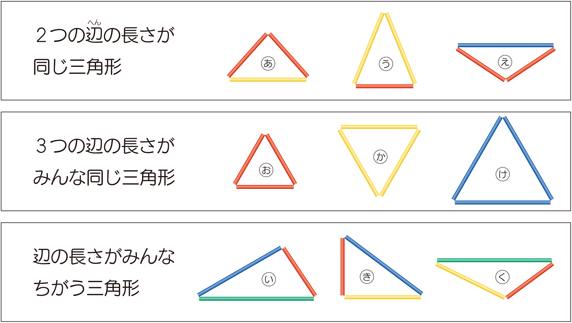



二等辺三角形と正三角形 算数用語集




1vec6 Abac Abc Descubre Como Resolverlo En Qanda




直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ
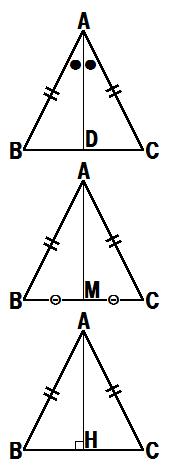



三角形の合同条件と二等辺三角形の底角 2 算数 数学記事



二等辺三角形の性質を利用した合同の証明 チーム エン




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形と正三角形 算数用語集




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者




無料 中2数学 発展問題 解答プリント 228 三角形 四角形1 二等辺三角形



直角二等辺三角形とは 定義や辺の長さの比 面積の求め方 受験辞典



中学数学 証明 二等辺三角形の性質の利用 中学数学の無料オンライン学習サイトchu Su



正三角形 二等辺三角形 直角三角形の書き方 作図 まとめ 受験辞典



5 0 Abczb Descubre Como Resolverlo En Qanda




この3問がどうしても わかりません 回答お願いいたします もしよければ途中経過も Clear



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




この問題の仮定と結論ってどれですか あと 解き方 教えてください Clear




Tossランド 二等辺三角形になるための条件



斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める
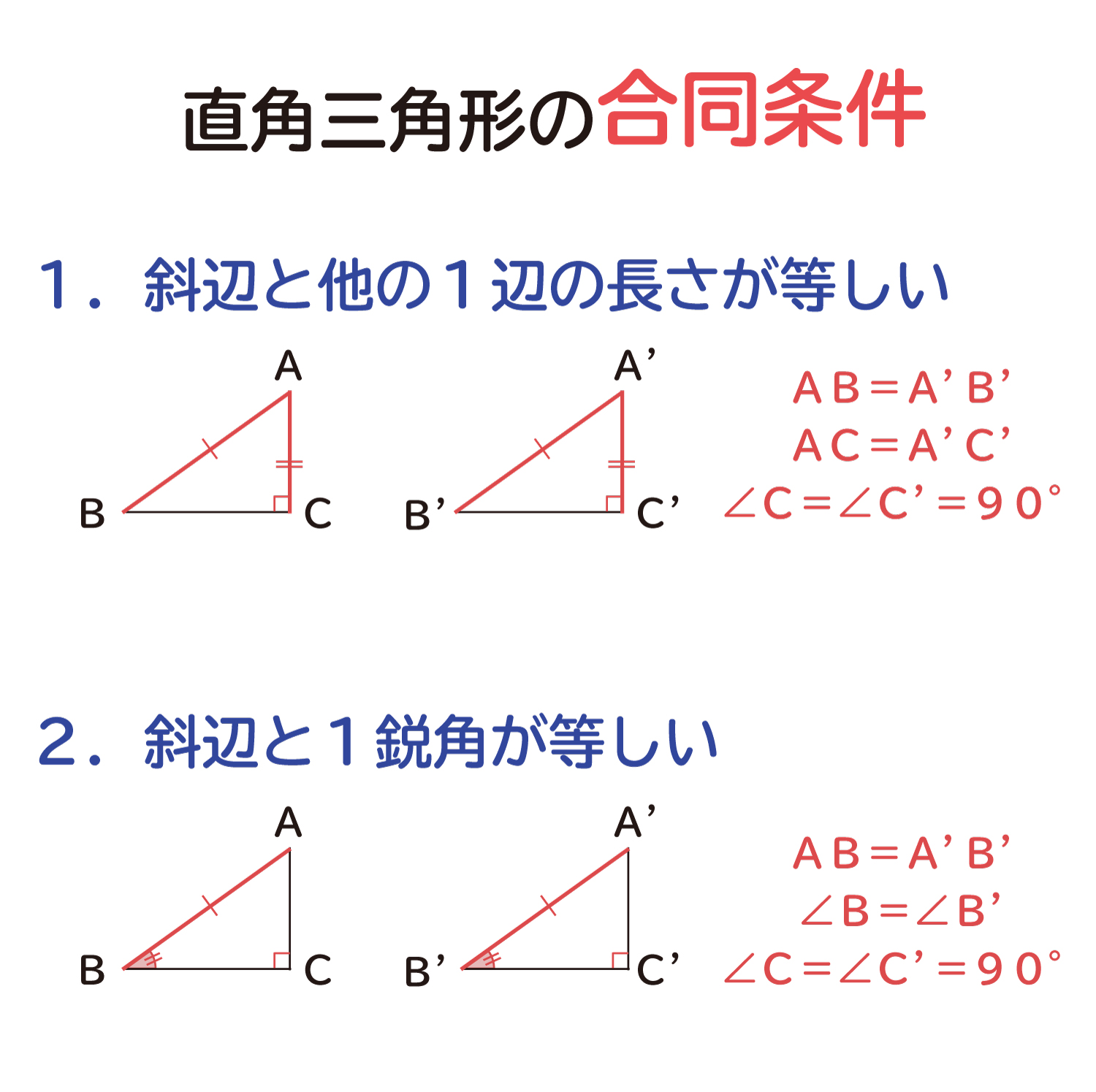



直角三角形の合同条件の説明 おかわりドリル
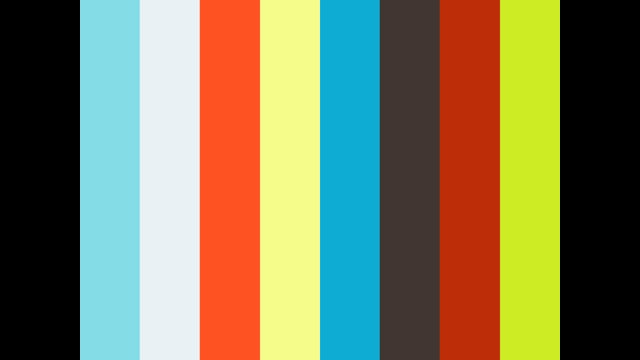



2 57第4章 二等辺三角形 二等辺三角形になるための条件 プログラミングの雫




A 4 4 Abac Abc Descubre Como Resolverlo En Qanda




中2 二等辺三角形になるための条件 中学生 数学のノート Clear
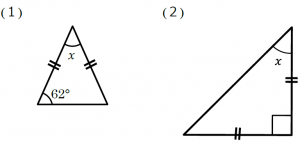



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン




ユニーク二 等辺 三角形 に なる 条件 最高のぬりえ
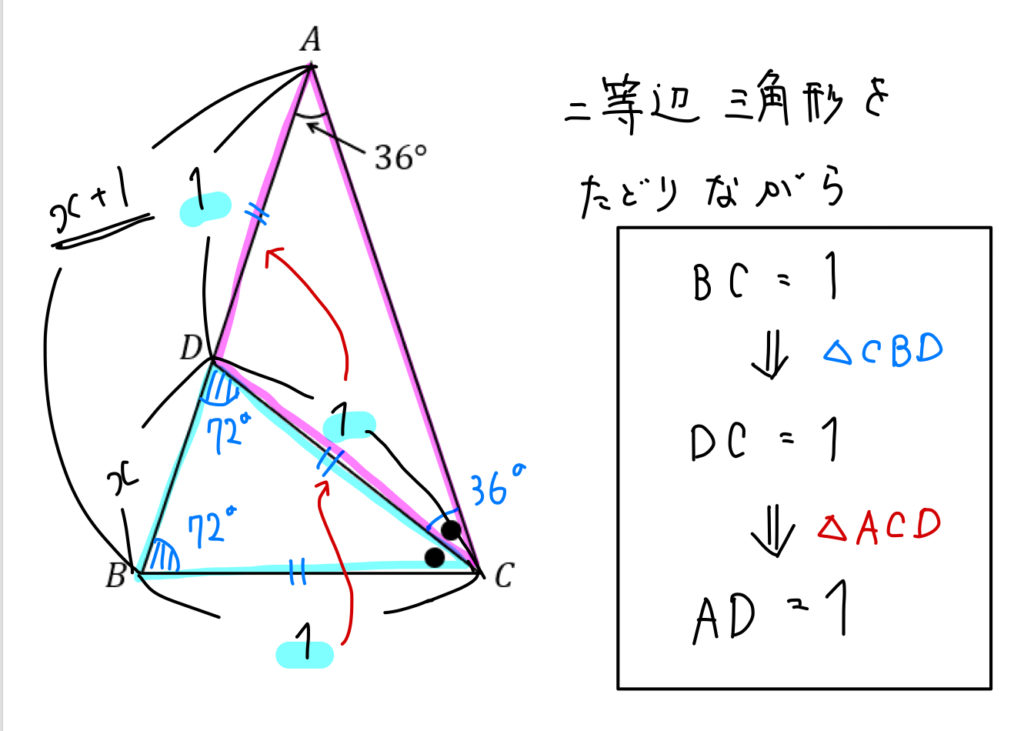



数学 36 の三角比 二等辺三角形を用いて求める方法は 数スタ



Http Cms Oklab Ed Jp Jh Rokuhoku Index Cfm 1 1423 C Html 1423 1217 Pdf




三角形の成立条件を理解するたった1つのポイント わかりやすく解説 遊ぶ数学



この問題の解き方を教えてください 右の図は Ab Acの二等辺三角形 Yahoo 知恵袋




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ




2 P P90 91 See How To Solve It At Qanda




二等辺三角形 Wikipedia
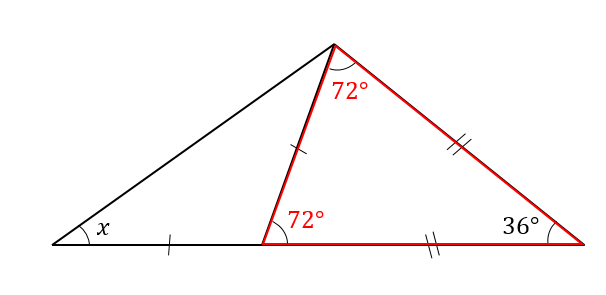



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




二等辺三角形になることの証明 Youtube
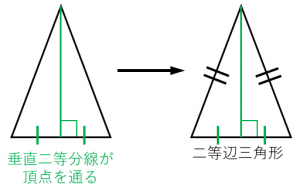



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
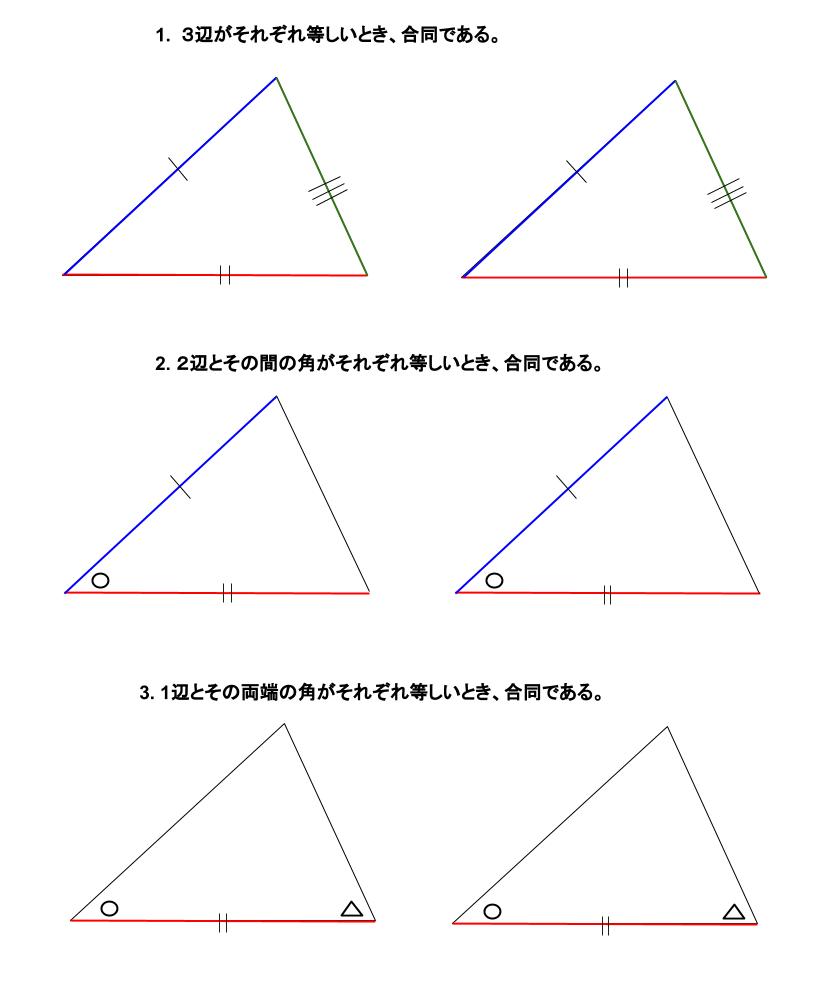



中学数学 三角形の合同条件 中学数学の無料オンライン学習サイトchu Su




中2数学 三角形 直角三角形の合同条件の覚え方のポイントを解説 まなビタミン



3年算数三角形教え方のポイント




二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学




スタディピア 図形




二等辺三角形の性質 Youtube
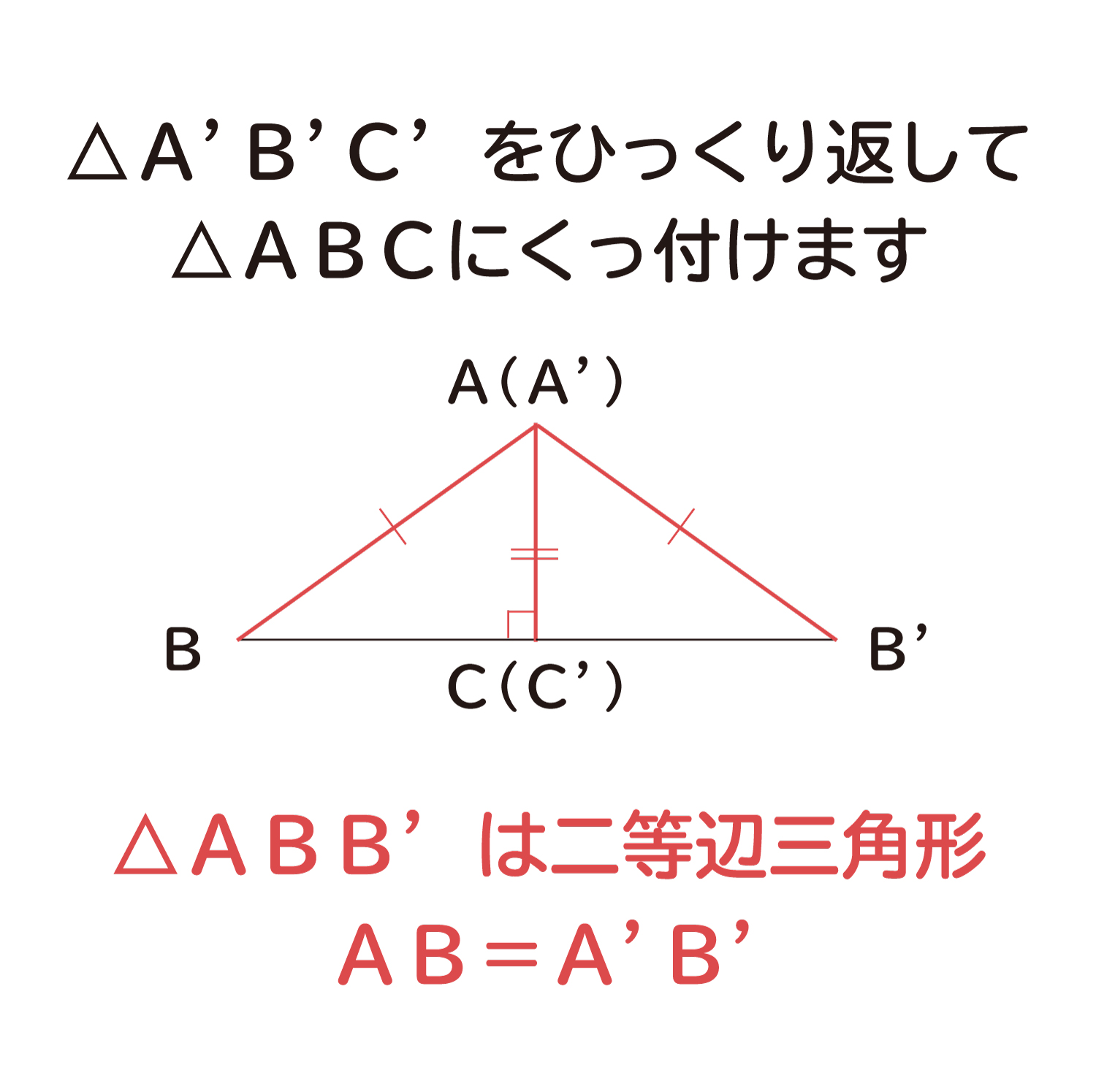



直角三角形の合同条件の説明 おかわりドリル




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく
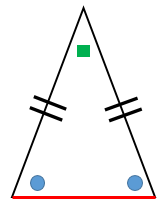



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




合同な図形 二等辺三角形の証明問題 苦手な数学を簡単に
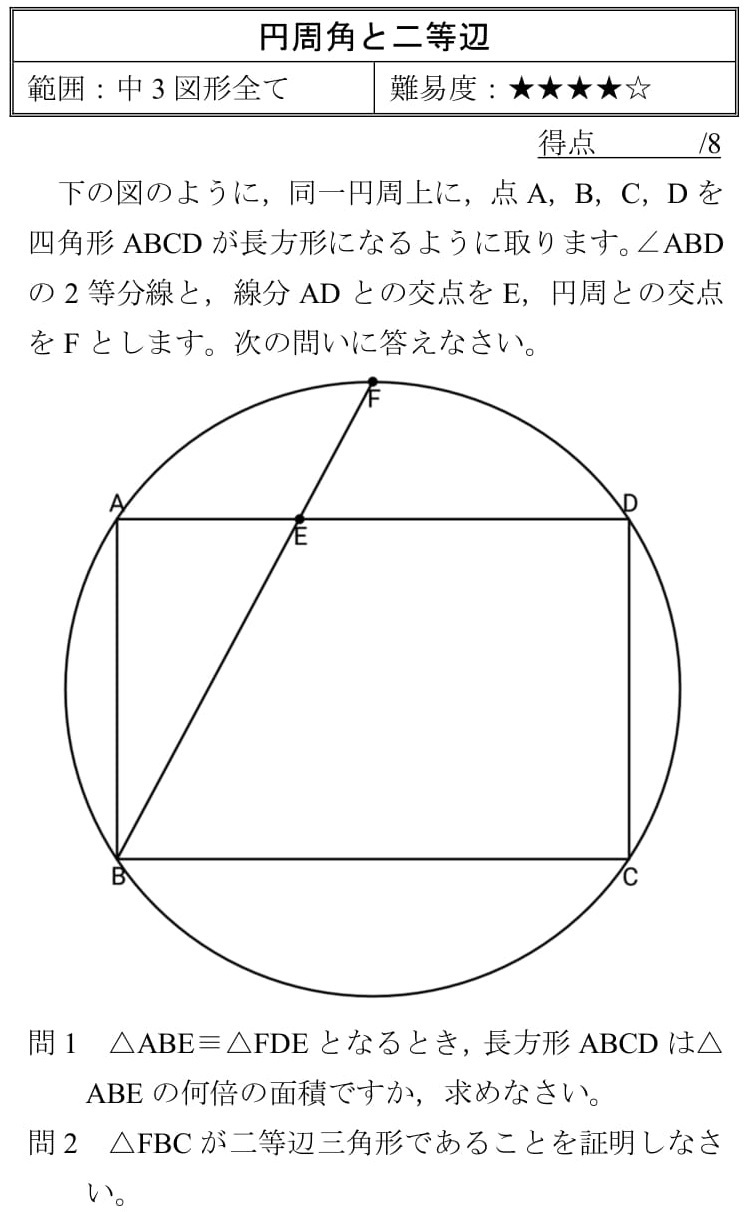



円周角と二等辺三角形 オリジナル 高校入試 数学 良問 難問



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




中2数学 二等辺三角形の3大重要ポイント 映像授業のtry It トライイット




三角形の相似条件 証明の練習になる簡単な問題を紹介 中学や高校の数学の計算問題




相似15 二等辺三角形 Youtube
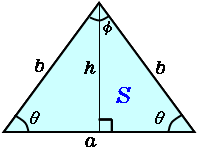



二等辺三角形 高精度計算サイト
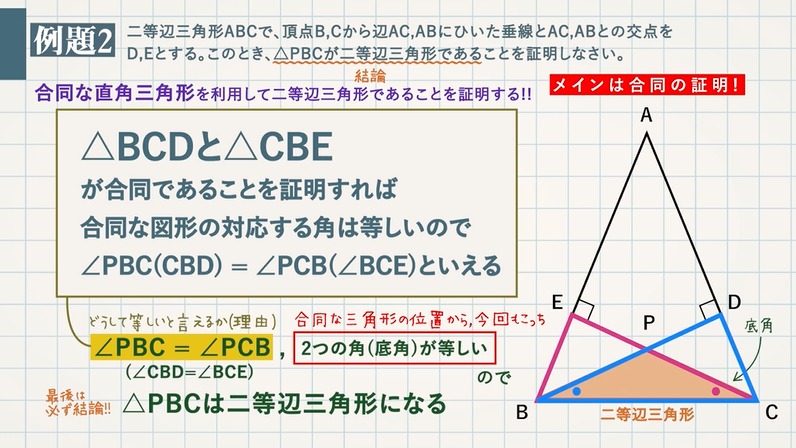



二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典




二等辺三角形の定理の証明がわかる3ステップ Qikeru 学びを楽しくわかりやすく



1




直角三角形の合同条件 算数 数学が好きになりmath




二等辺三角形になるための条件 Youtube




直角三角形の合同条件とその証明 数学fun




二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4



中2数学 2角が等しい三角形 二等辺三角形の長さを用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト




二等辺三角形で 底辺の内分点と頂点の距離は Mr の数学と古美術




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学
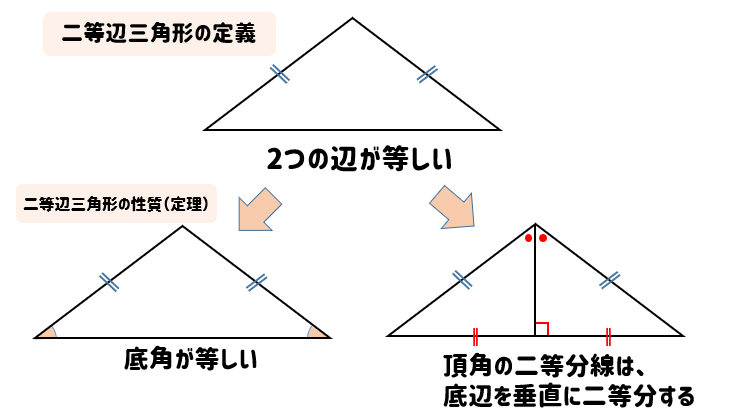



二等辺三角形の定義と性質をサクッと確認しておこう 数スタ



1



二等辺三角形ができる条件
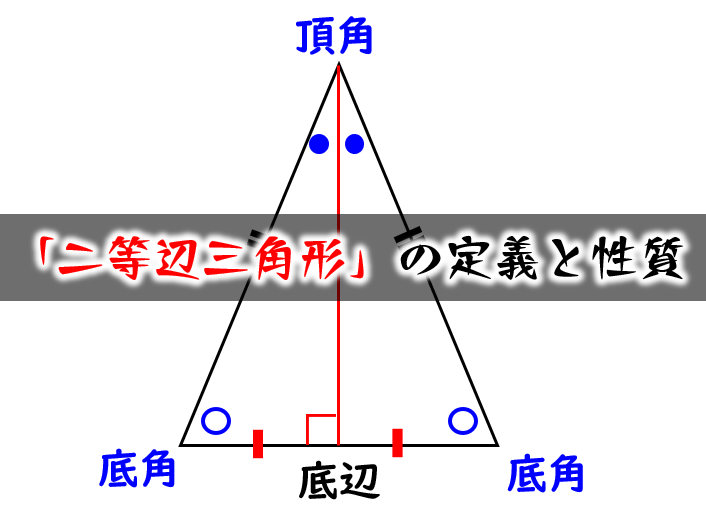



二等辺三角形の定義と性質 問題の解き方 数学fun



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学
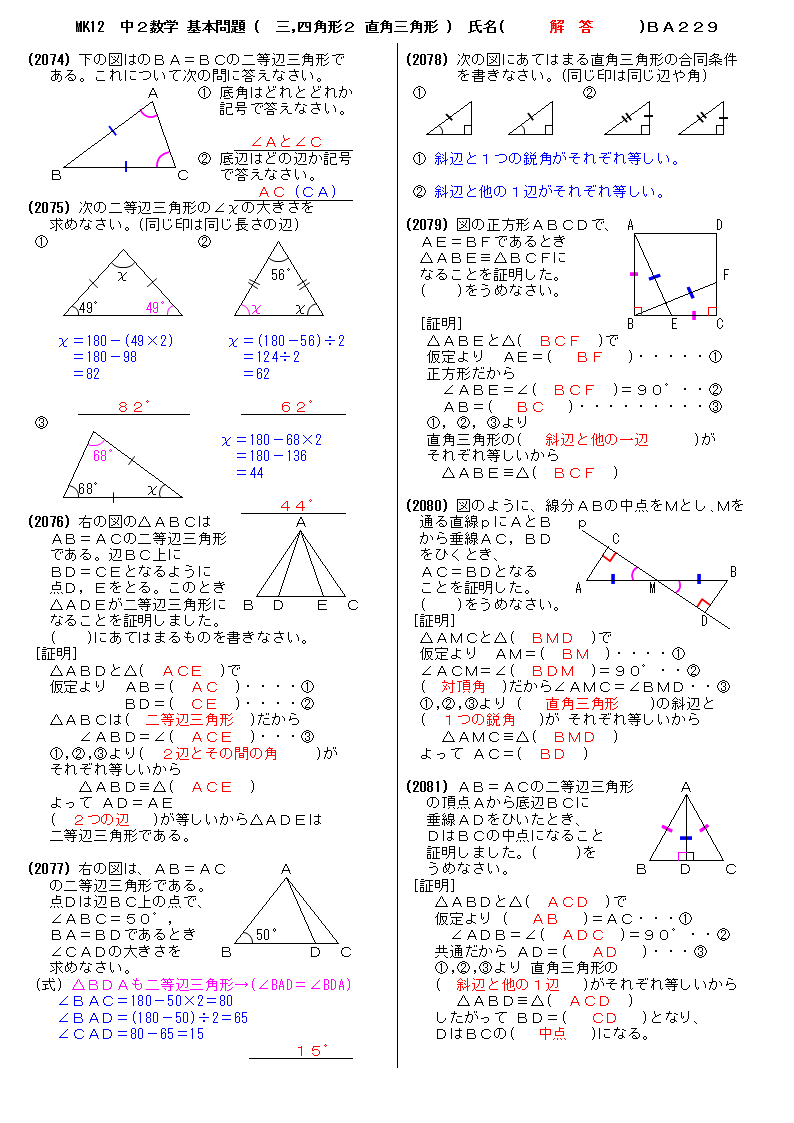



無料 中2数学 基本問題 解答プリント 229 三角形 四角形2 直角三角形
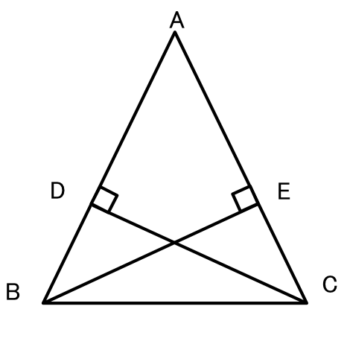



フロー 2 5 4 4 直角三角形の合同条件を利用した証明
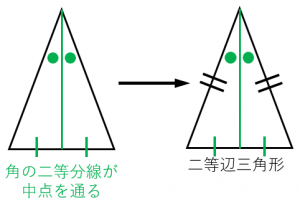



二等辺三角形の4つの性質と4つの条件 具体例で学ぶ数学




二等辺三角形になるための条件 Youtube
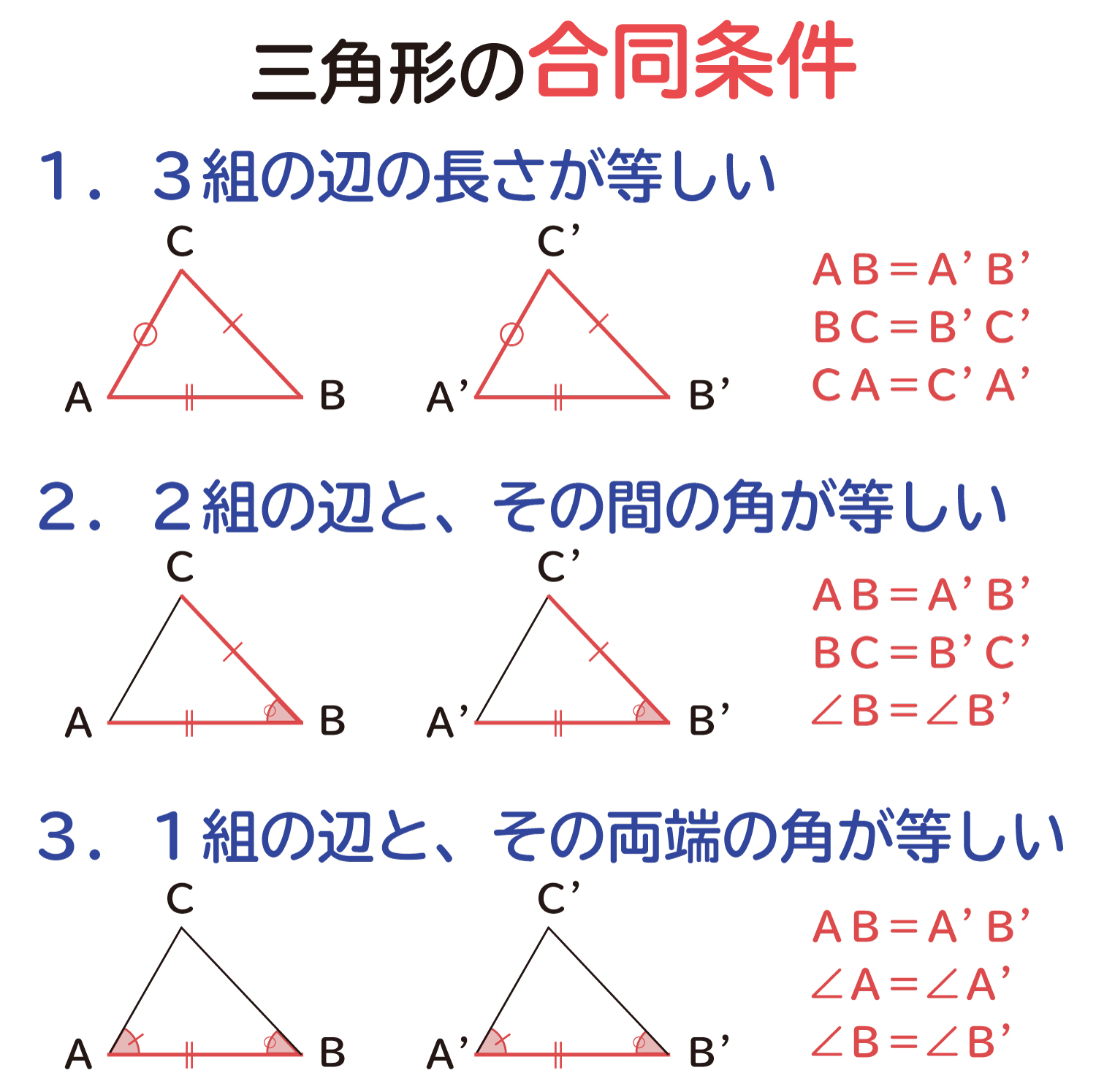



三角形の合同条件の説明 おかわりドリル



二等辺三角形の性質 まなびの学園



3



中学数学証明問題です 直角三角形の合同条件はわかるのですが Yahoo 知恵袋




二等辺三角形の性質と証明 無料で使える中学学習プリント




簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




P117 4 Zbad Zcad Ad Ec E Descubre Como Resolverlo En Qanda



数学 二等辺三角形になるための条件 タイトル この問題 Yahoo 知恵袋



0 件のコメント:
コメントを投稿