Click here👆to get an answer to your question ️ Using binomial theorem, expand {(x y)^5 (x y)^5} and hence find the value of {(√(2) 1)^5 (√(2) 1)^5 }Binomials raised to a power A binomial is a polynomial with two terms We're going to look at the Binomial Expansion Theorem, a shortcut method of raising a binomial to a power (xy) 0 = 1 (xy) 1 = x y (xy) 2 = x 2 2xy y 2 (xy) 3 = x 3 3x 2 y 3xy 2 y 3 (xy) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4So in this particular case we get (x y)6 = 6C0x6 6C1x6−1y1 6C2x6−2y2 6C3x6−3y3 6C4x6−4y4 6C5x6−5y5 6C6y6 = x6 6x5y 15x4y2 x3y3 15x2y4

11 1 Pascal S Triangle And The Binomial Theorem Ppt Download
What is the formula for binomial expansion
What is the formula for binomial expansion-2903 · Definition binomial A binomial is an algebraic expression containing 2 terms For example, (x y) is a binomial We sometimes need to expand binomials as follows (a b) 0 = 1(a b) 1 = a b(a b) 2 = a 2 2ab b 2(a b) 3 = a 3 3a 2 b 3ab 2 b 3(a b) 4 = a 4 4a 3 b 6a 2 b 2 4ab 3 b 4(a b) 5 = a 5 5a 4 b 10a 3 b 2 10a 2 b 3 5ab 4 b 5Clearly, · Binomial expression is an algebraic expression with two terms only, eg 4x 2 9 When such terms are needed to expand to any large power or index say n, then it requires a method to solve it Therefore, a theorem called Binomial Theorem is introduced which is an efficient way to expand or to multiply a binomial expressionBinomial Theorem is defined as the



3 6 Pascal S Triangle And The Binomial Theorem Mathematics Libretexts
⋅(x)12−k ⋅(−y)k ∑ k = 0 12 Expand binomials using the binomial expansion method stepbystep full pad » x^2 x^ {\msquare} \log_ {\msquare} \sqrt {\square} \nthroot \msquare {\square} \le \ge( 13 − 1)!
According to the binomial formula ( a b) n = ∑ k = 0 n n C k ( a n − k b k) So ( x y) 1 3 = ∑ k = 0 1 3 1 3 C k ( ( x) 13 − k ( y) k) By expanding the summation 13!X, y ∈ R;N ∈ N Then the result will be \\sum_{i=0}^{n}nC_rx^{nr}y^r nC_rx^{nr}y^r nC_{n1}xy^{n1} nC_ny^n\
Expanding a binomial with a high exponent such as (x 2 y) 16 (x 2 y) 16 can be a lengthy process Sometimes we are interested only in a certain term of a binomial expansion We do not need to fully expand a binomial to find a single specific term Note the pattern of coefficients in the expansion of (x y) 5 (x y) 5Binomial Theorem Calculator online with solution and steps Detailed step by step solutions to your Binomial Theorem problems online with our math solver and calculator Solved exercises of Binomial Theorem · The binomial expansion of (x^2y)^2 is?
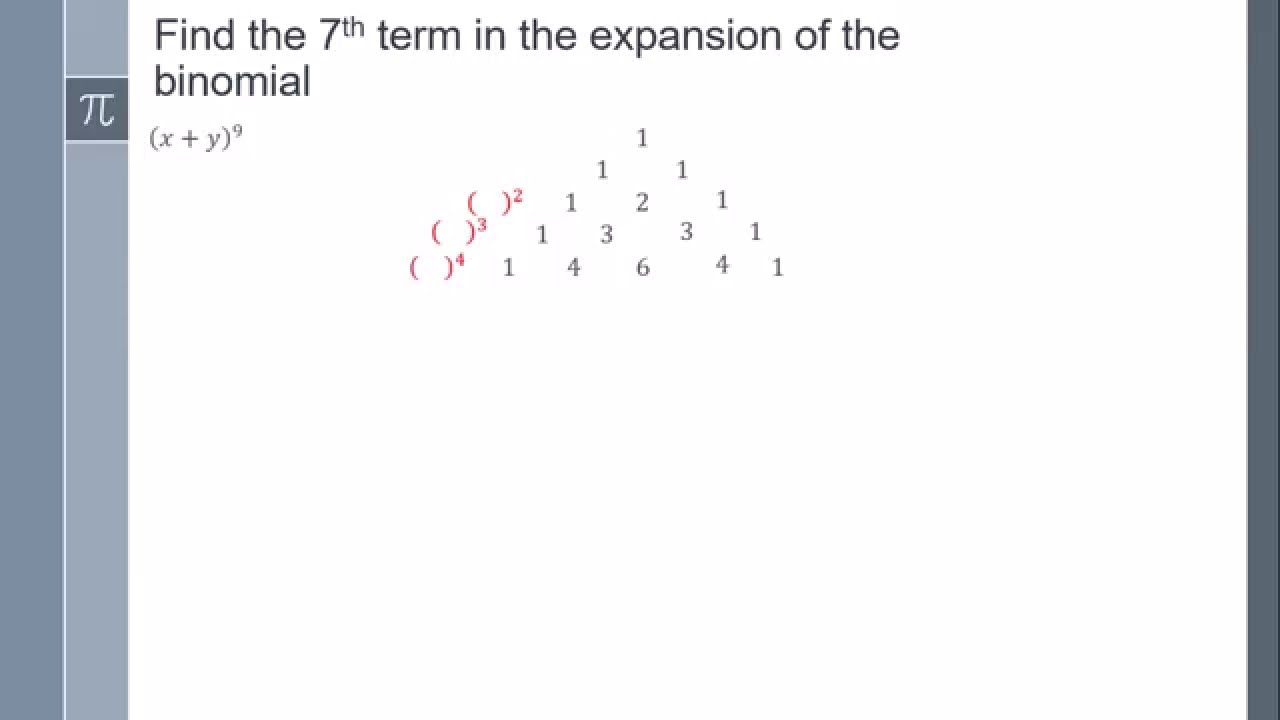


Find The 7th Term In The Expansion Of The Binomial Youtube
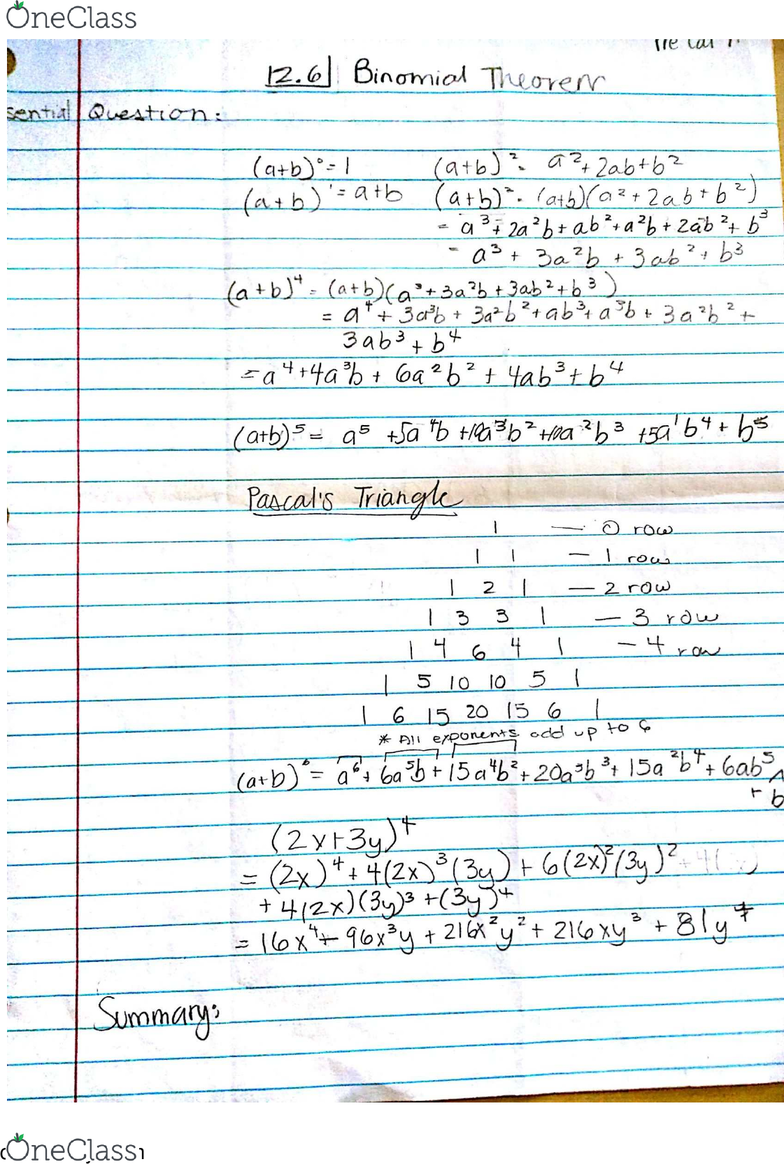


Math 1 Lecture 3 Using The Binomial Theorem Oneclass
Binomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Notice that the powers are descending in x and ascending in yAlthough FOILing is one way to solve these problems, there is a much easier way( x) 13 − 1 × ( y) 1 13!( x) 13 − 0 × ( y) 0 13!
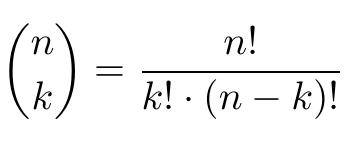


Binomial Coefficient Calculator



Binomial Theorem Ck 12 Foundation
Find the expansion of (xy)^{4} a) using combinatorial reasoning, as in Example 1 b) using the binomial theoremExpand (x 2 3) 6;A Level Pure Maths revision tutorial videoFor the full list of videos and more revision resources visit wwwmathsgeniecouk
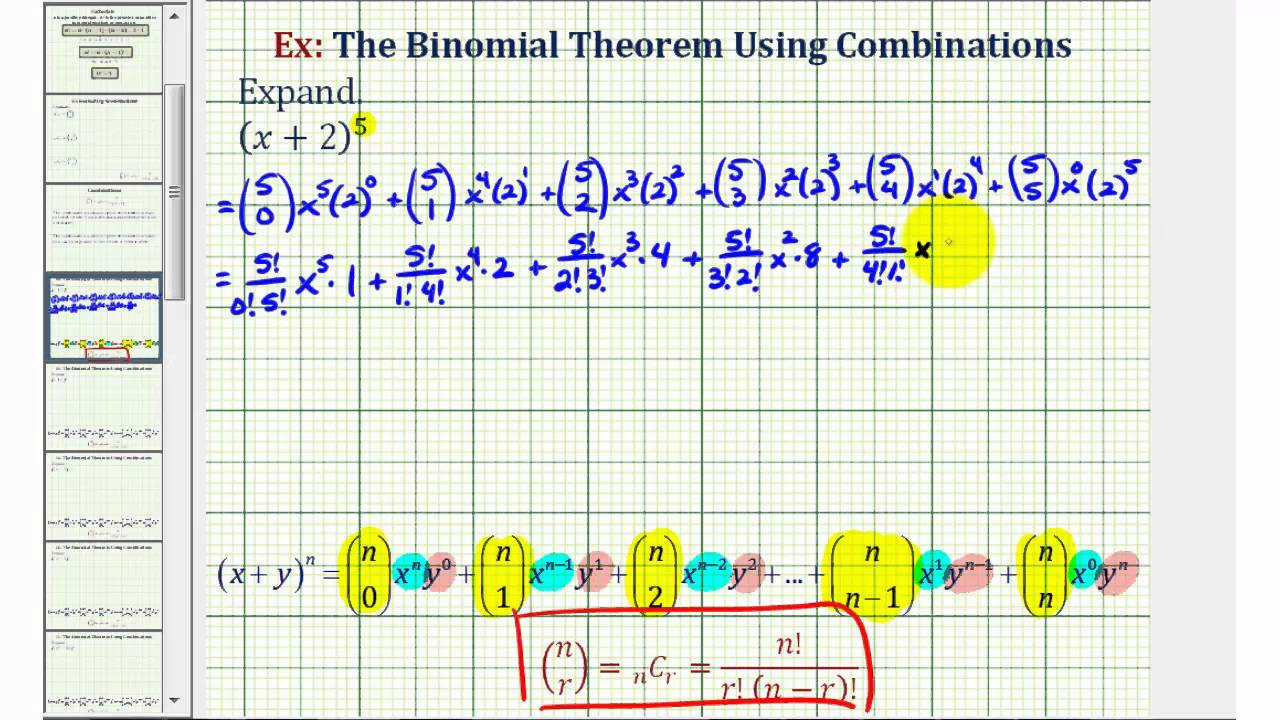


Binomial Theorem Solutions Examples Videos
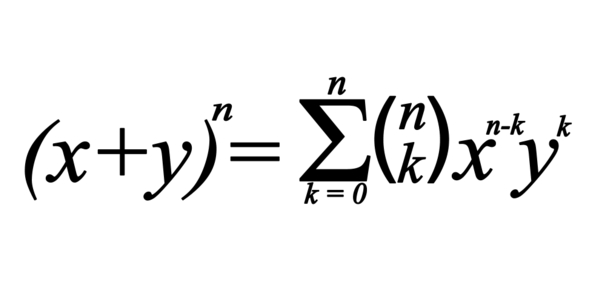


Binomial Theorem Quiz Proprofs Quiz
Use the Binomial Theorem to Expand a Binomial We are now ready to use the alternate method of expanding binomials The Binomial Theorem uses the same pattern for the variables, but uses the binomial coefficient for the coefficient of each term( 4 k)!The binomial theorem revisited The binomial theorem, as stated in the previous section, was only given for n as a whole positive number We can now find the binomial expansion for (1 x) n for all values of n using the Maclaurin series f(x) = (1 x)n f′ ( x) = n (1 x) n−1 f ″ ( x) = n ( n − 1) (1 x



Binomial Theorem Read Probability Ck 12 Foundation



The Normal Drawn On The Curve Xy 12 At Point 3t 4 T Cut T
Sounds like we want to use pascal's triangle and keep track of the x^2 term We can skip n=0 and 1, so next is the third row of pascal's triangle 1 2 1 for n = 2 the x^2 term is the rightmost one here so we'll get 1 times the first term to the 0 power times the second term squared or 1*1^0* (x/5)^2 = x^2/25 so not here 1 3 3 1 for n = 3⋅ ( X) 4 k ⋅ ( Y(MIDDLE SCHOOL MATH) For a school dance, a section of the gym, in the shape of a trapezoid, has



How Do You Use The Binomial Series To Expand 1 X 12 Socratic



Chapter 3 The Binomial Theorem Pages 1 14 Flip Pdf Download Fliphtml5
2700 · Binomial Theorem Expansion In binomial theorem expansion, the binomial expression is most important in an algebraic equation which holds two different terms Such as a b, a 3 b 3, etc Let's consider;En matemáticas, el teorema del binomio es una fórmula que proporciona el desarrollo de la ésima potencia de un binomio, siendo De acuerdo con el teorema, es posible expandir la potencia () en una suma que implica términos de la forma , donde los exponentes ,, es decir, son números naturales con =, y el coeficiente de cada término es un número entero positivo que depende de y4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n



Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11



Elementary Algebra And Geometry Crc Press Online Binomial Theorem For Positive Integer N Xy Xy Nn Xy Nn N Xy Nxy Nn Nn N N 12 2 33 1 2 12 3 1 Yn Pqzshienbsbmbzmpssbodt Pdf Document
1600 · Expand (3x2y)^12 using binomial theorem and find coefficient of x^5 y^7 * Get the answers you need, now!Binomial Theorem Tutorial Binomial expression An algebraic expression consisting of two terms with a positive or negative sign between them is called a binomial expression Example (ab), ( P / x 2) – (Q / x 4) etc Binomial Theorem When a binomial expression is raised to a power 'n' we would like to be able to expand it👉 Learn how to expand a binomial using binomial expansion A binomial expression is an algebraic expression with two terms When a binomial expression is ra



If X Y 4 And Xy 12 Find X3 Y3 Chapter 2 Class 9 Maths Polynomials Polynomials Class 9 Youtube
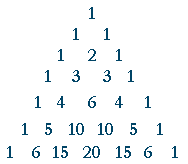


Binomial Theorem Topics In Precalculus
· Explanation The Binomial Theorem gives a time efficient way to expand binomials raised to a power and may be stated as (x y)n = n ∑ r=0nCrxn−ryr, where the combination nCr = n!( 13 − 3)!( 13 − 0)!
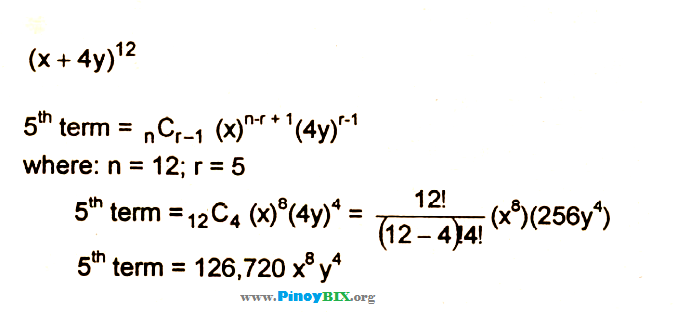


Solution In The Expression Of X 4y 12 What Is The Numerical Coefficient Of



Pascal S Triangle And The Coefficients In The Expansion Of Binomials Ck 12 Foundation
0800 · In algebra, a binomial is an algebraic expression with exactly two terms (the prefix 'bi' refers to the number 2) If a binomial expression (x y)n is to be expanded, a binomial expansion formula can be used to express this in terms of the simpler expressions of the form ax by c in which 'b' and 'c' are non negative integers · Evaluate a Binomial Coefficient While Pascal's Triangle is one method to expand a binomial, we will also look at another method Before we get to that, we need to introduce some more factorial notationThis notation is not only used to expand binomials, but also in the study and use of probabilityStudents trying to do this expansion in their heads tend to mess up the powers But this isn't the time to worry about that square on the xI need to start my answer by plugging the terms and power into the TheoremThe first term in the binomial is "x 2", the second term in "3", and the power n is 6, so, counting from 0 to 6, the Binomial Theorem gives me



9 5 The Binomial Theorem Lets Look At
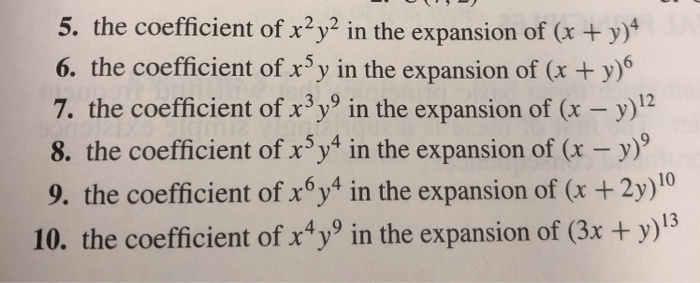


Solved 5 The Coefficient Of X2y2 In The Expansion Of X Chegg Com
( 13 − 2)!Using the Binomial Theorem When we expand ( x y) n \displaystyle {\left (xy\right)}^ {n} (x y) n by multiplying, the result is called a binomial expansion, and it includes binomial coefficients If we wanted to expandX6 y3 (2)3 = 9!/ (3!



12 5 Binomial Theorem Mathematics Libretexts



Solved Algebra 2 Can Someone Please Check My Work And Co Chegg Com
After having gone through the stuff given above, we hope that the students would have understood "How to Find Coefficient of x in Binomial Expansion"Apart from the stuff given above, if you want to know more about "How to Find Coefficient of x in Binomial Expansion" Apart from the stuff given in this section, if you need any other stuff in math, please use our google custom search hereN C 3 = n C 12 If n C x = n Cy ==> x = y or x y = n n = 15 Question 3 If the binomial coefficients of three consecutive terms in the expansion of (a x) n23 Write out the binomial expansion of — — Show that one of the terms is independent of x Evaluating Expansions of Sums and Differences We can be asked to evaluate expansions such as (1 and write the answer in the form a bN6 Example Expand (3 N5)5 by the Binomial Theorem, and write your answer m the form a bü Solution



11 1 Pascal S Triangle And The Binomial Theorem Ppt Download



Example 7 Find Coefficient Of X6y3 In Expansion X 2y 9
初等代数学における二項定理(にこうていり、英 binomial theorem )または二項展開 (binomial expansion) は二項式の冪の代数的な展開を記述するものである。 定理によれば、冪 (x y) n は a x b y c の形の項の和に展開できる。 ただし、冪指数 b, c は b c = n を満たす非負整数で、各項の係数 aYou can expand the given term (x y)12 in a binomial expansion by using Newton's binomial theorem & the formula of it 2 What is the Binomial Expansion of (x y)12?A = x And substitute that into the binomial expansion (1a)^n This yields exactly the ordinary expansion Then, by substituting x for a, we see that the solution is simply the ordinary binomial expansion with alternating signs, just as everyone else has suggested



Binomial Theorem And Expansions Read Probability Ck 12 Foundation



Pencil Red Pen Highlighter Gp Notebook Calculator Ppt Download
Expand Using the Binomial Theorem (xy)^12 (x − y)12 ( x y) 12 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n n C k ⋅ ( a n k b k) 12 ∑ k=0 12! · Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeExpand Using the Binomial Theorem (XY)^4 (X Y)4 ( X Y) 4 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n n C k ⋅ ( a n k b k) 4 ∑ k=0 4!



Binomial Expansion Theorem Notes Guided Examples Practice X Y Tpt



Solved Problem 9 3 3 6 Points A Use The Binomial T Chegg Com
The binomial expansion calculator is used to solve mathematical problems such as expansion, series, series extension, and so on Before getting details about how to use this tool and its features to resolve the theorem, it is highly recommended to know about individual terms such as binomial, extension, sequences, etcNotice that the entire right diagonal of Pascal's triangle corresponds to the coefficient of latexy^n/latex in these binomial expansions, while the next diagonal corresponds to the coefficient of latexxy^{n−1}/latex and so on Example Find the expansion of latex(xy)^5/latex using Pascal's triangle⋅(X)4−k ⋅(Y)k ∑ k = 0 4 4!



8 5 The Binomial Theorem Mathematics Libretexts



The Binomial Theorem Binomial Expansions Using Pascal S Triangle Subsets Binomial Theorem Theorems Pascal S Triangle
Binomial Expansion Calculator The calculator will find the binomial expansion of the given expression, with steps shown Binomial Power If the calculator did not compute something or you have identified an error, or you have a suggestion/feedback, please write it in the comments below · 10 CHAPTER OBJECTIVE 6 Single Answer Correct LEVELI 1 The coefficient ofr y ,yzt2 andxyzt in the expansion of (x Y z t) 4 are the ratioBinomial Expansion Calculator is a free online tool that displays the expansion of the given binomial term BYJU'S online binomial expansion calculator tool makes the calculation faster, and it displays the expanded form in a fraction of seconds



Binomial Theorem For Any Index



Q Fnd The Coeff Of X9y 3inthe Expansion Of 2x2 Y Y 3x 12 Maths Binomial Theorem Meritnation Com
2703 · In algebra, the algebraic expansion of powers of a binomial is expressed by binomial expansion In binomial expansion, a polynomial (x y) n is expanded into a sum involving terms of the form a x b y c, where b and c are nonnegative integers, and the coefficient a is a positive integer depending on the value of n and bThis information can be summarized by the Binomial Theorem For any positive integer n, the expansion of (x y)n is C(n, 0)xn C(n, 1)xn1y C(n, 2)xn2y2 C(n, n 1)xyn1 C(n, n)yn Each term r in the expansion of (x y)n is given by C(n, r 1)xn (r1)yr1 Example Write out the expansion of (x y)70118 · MGSE9‐12AAPR5 Know and apply that the Binomial Theorem gives the expansion of (x y)n in powers of x and y for a positive integer n, where x and y are any numbers, with coefficients determined using Pascal's Triangle Vocabulary Binomial Expansion – Finding the polynomial of a binomial raised to a power greater than 1 Pascal's



6 Binomial Theorem Example 2 Finding The Term Independent Of X Youtube



Solved 6 Binomial Theorem Applications 15 Points A Chegg Com
( x) 13 − 2 × ( y) 2 13!The Binomial Expansion of (x y)12 is x12 12x11y 66x10y2 2x9y3 495x8y4 792x7y5 924x6y6 792x5y7 495x4y8 2x3y9 66x2y10 12xy11 y122901 · We know that General term of expansion (a b)n is Tr1 = nCr an–r br For (x 2y)9, Putting n = 9 , a = x , b = 2y Tr 1 = 9Cr (x)9 – r (2y)r = 9Cr (x)9 – r (y)r (2)r We need to find coefficient of x6 y3 Comparing yr = y3 r = 3 Putting r = 3 in (1) T31 = 9C3 x9 – 3 y3 (2)3 = 9!/3!



How Do You Expand X Y 6 Using Pascal S Triangle Socratic



Precalculus Name Notes On The Binomial Theorem 10 4 13 I
6!) (2)3 x6 y3



Digital Lesson The Binomial Theorem The Binomial Theorem



Expand X 2 2y 5 Using Binomial Expansion Youtube



In The Expansion Of X Y N If The Binomial Coefficient Of The Th



Solved 12 Use The Binomial Theorem To Find The Coefficie Chegg Com



Find Middle Term For Even Power Binimial Expansion Youtube



What Is The Third Term Of The Binomial Expansion Math 2x Y 6 Math Quora



The Binomial Theorem



Using The Binomial Theorem College Algebra



Ib Hl Math Homework 2 Logs Binomial Theorem And Induction



Solved Use The Binomial Theorem To Expand X Y 8 Find Chegg Com



Binomial Expansion Theorem Notes Guided Examples Practice X Y Tpt



What Is The Number Of Terms In The Expansion Of Math X Y Z 12 Math Quora



Using The Binomial Theorem College Algebra



The Binomial Theorem



8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download



Binomial Theorem Wikipedia



Solved Section 3 3 Binomial Coefficients 30 Points 5 Bon Chegg Com


1 Expand X Y 5 Using Binomial Theorem Youtube
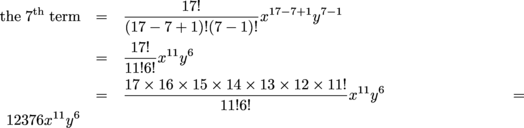


Pascal S Triangle And The Binomial Theorem At A Glance



8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



The Sum Of All The Coefficients Of The Terms In The Expansion Of



Solved Question 9 In The Expansion Of X Y 24 Which Ter Chegg Com



9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download



The Binomial Theorem Boundless Algebra



A Quick And Efficient Way To Expand Binomials Ppt Download



Expand The Following By Binomial Theorem X Y 5



Binomial Theorem Solutions Examples Videos



8 5 The Binomial Theorem Warm Up Copyright C By Houghton Mifflin Company Inc All Rights Reserved 2 X Y 3 X 3 3x 2 Y 3xy 2 Y Ppt Download


4 The Binomial Theorem



Using Binomial Theorem Expand X Y 5 X Y And Hence Find The Value Of Root 2 1 5 Root 2 1 5 Maths Binomial Theorem Meritnation Com



Binomial Theorem Finding The Coefficient Of X 3 In 2 4x 5 Youtube



The Greatest Binomial Coefficient In The Expansion Of X 3 2 Y



Finding The 7th Term Of Binomial Expansion Youtube



Air Force Xy Vijaypath Batch Math By Vivek Rai Sir Binomial Theorem Class 12 Youtube


How To Expand X Y 7 Quora



9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download



Determine The Second Term Of The Binomial Expansion X Y 4 Brainly Com



Answered X Y 10 4 10 6 40 X 41 X 6y N Bartleby



Understanding Binomial Expansion Mathematics Stack Exchange



Don T Understand Why This Binomial Expansion Is Not Valid For X 1 Mathematics Stack Exchange



Binomial Theorem Wikipedia



Pascal S Triangle And The Binomial Theorem At A Glance



Ex 8 2 5 Find 4th Term Of X 2y 12 Chapter 8 Class 11



The Binomial Theorem Ppt Download



Ppt The Binomial Theorem Powerpoint Presentation Free Download Id



Find The 6th Term In The Expansion Of 2x Y 12 Brainly In
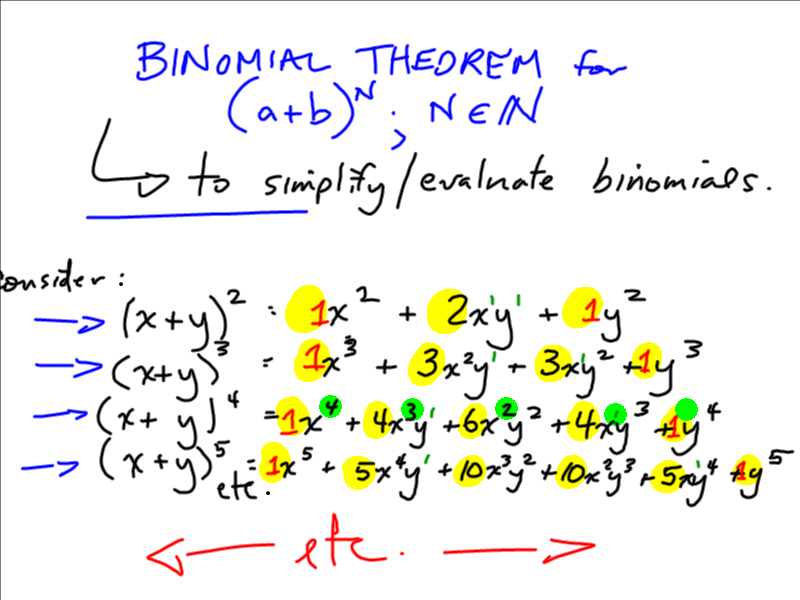


Grade 12 Pre Calculus Math 0910 Binomial Theorem



3 6 Pascal S Triangle And The Binomial Theorem Mathematics Libretexts



Binomial Theorem Find Term Containing X 6 Youtube



Binomial Theorem



Digital Lesson The Binomial Theorem The Binomial Theorem



9 5 The Binomial Theorem Let S Look At The Expansion Of X Y N Ppt Video Online Download


Find The Coefficient Of X 5 In The Binomial Expansion Of X 4 3x 1 6 Two Binomials Youtube


What Is The Number Of Terms In The Expansion Of Math X Y Z 12 Math Quora


12 4 Binomial Theorem Teacher Guide



Alg2 March28 The Answers
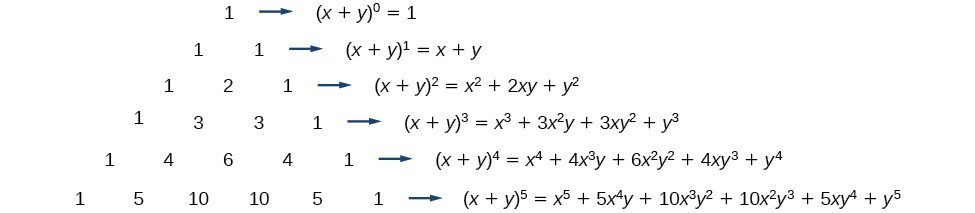


Using The Binomial Theorem College Algebra


5 7 The Binomial Theorem Parks Act Questions For Ica



Binomial Theorem Properties Terms In Binomial Expansion Examples Pdf



0 件のコメント:
コメントを投稿